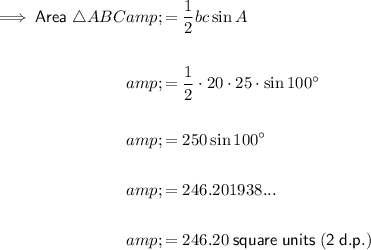Question

NO LINKS!!!! URGENT HELP PLEASE!!!!!

Find the area of ΔABC

5. B= 141°, a = 7, c = 8

6. C=70°, a=30, b= 24

7. A = 100°, b = 20, c = 25

Answer 1

5) 17.62 units² (2 d.p.)

6) 338.29 units² (2 d.p.)

7) 246.20 units² (2 d.p.)

Explanation:

To find the area of a triangle given two sides and the included angle, use the Sine Rule (Area of a Triangle) formula:

`\boxed{\begin{minipage}{6 cm}\underline{Sine Rule (Area of a triangle)}\\\\$A=(1)/(2)ab \sin C$\\\\\\where: \\ \phantom{ww}$\bullet$ $a$ and $b$ are adjacent sides. \\ \phantom{ww}$\bullet$ $C$ is the includ\:\!ed angle.\\\end{minipage}}`

`\hrulefill`

Question 5

Given values:

• a = 7
• c = 8
• B = 141°

The two sides of the triangle are 'a' and 'c', and the included angle is 'B'.

Substitute the given values into the formula and solve for area:

`\begin{aligned}\implies \textsf{Area}\; \triangle ABC&=(1)/(2) ac \sin B\\\\&=(1)/(2) \cdot 7 \cdot 8 \cdot \sin 141^(\circ)\\\\&= 28 \sin 141^(\circ)\\\\& = 17.6209709...\\\\&= 17.62\; \sf square\;units\;(2\;d.p.)\end{aligned}`

`\hrulefill`

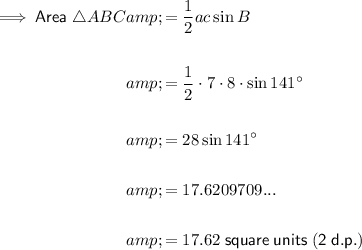
Question 6

Given values:

• a = 30
• b = 24
• C = 70°

The two sides of the triangle are 'a' and 'b', and the included angle is 'C'.

Substitute the given values into the formula and solve for area:

`\begin{aligned}\implies \textsf{Area}\; \triangle ABC&=(1)/(2) ab \sin C\\\\&=(1)/(2) \cdot 30\cdot 24 \cdot \sin 70^(\circ)\\\\&= 360\sin 70^(\circ)\\\\&= 338.289343...\\\\& = 338.29\; \sf square\;units\;(2\;d.p.)\end{aligned}`

`\hrulefill`

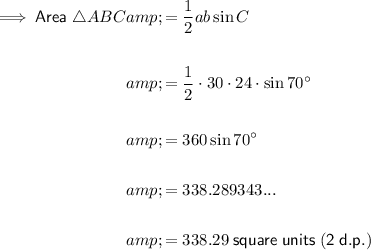
Question 7

Given values:

• b = 20
• c = 25
• A = 100°

The two sides of the triangle are 'b' and 'c', and the included angle is 'A'.

Substitute the given values into the formula and solve for area:

`\begin{aligned}\implies \textsf{Area}\; \triangle ABC&=(1)/(2) bc \sin A\\\\&=(1)/(2) \cdot 20 \cdot 25 \cdot \sin 100^(\circ)\\\\&= 250 \sin 100^(\circ)\\\\&= 246.201938...\\\\& = 246.20\; \sf square\;units\;(2\;d.p.)\end{aligned}`