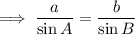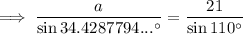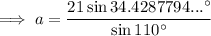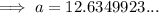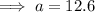Question

NO LINKS!!!! URGENT HELP PLEASE!!!!!

Solve ΔABC using the Law of Sines Part 1

3. A = 110°, a= 14, b= 9

4. B = 110°, c = 13, b = 21

Answer 1

3) B = 37.2°, C = 32.8°, c = 8.1

4) A = 34.4°, C = 35.6°, a = 12.6

Explanation:

To solve for the remaining sides and angles of the triangle, given two sides and an adjacent angle, use the Law of Sines formula:

`\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}`

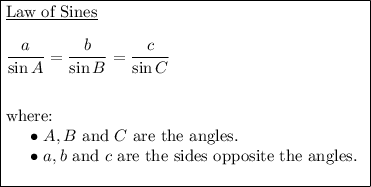
Question 3

Given values:

• a = 14
• b = 9
• A = 110°

Substitute the given values into the formula and solve for angle B:

`\implies (a)/(\sin A)=(b)/(\sin B)`

`\implies (14)/(\sin 110^(\circ))=(9)/(\sin B)`

`\implies 14\sin B=9\sin 110^(\circ)`

`\implies \sin B=(9\sin 110^(\circ))/(14)`

`\implies B=\sin^(-1)\left((9\sin 110^(\circ))/(14)\right)`

`\implies B=37.1632517...^(\circ)`

`\implies B=37.2^(\circ)`

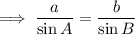
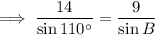
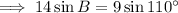
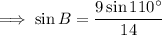
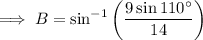
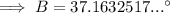
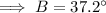
As the interior angles of a triangle sum to 180°:

`\implies A+B+C=180^(\circ)`

`\implies C=180^(\circ)-A-B`

`\implies C=180^(\circ)-110^(\circ)-37.1632517...^(\circ)`

`\implies C=32.8367482...^(\circ)`

`\implies C=32.8^(\circ)`

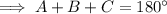
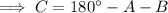
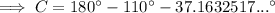
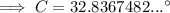
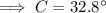
Finally, substitute the values of a, A, and C into the Law of Sines formula and solve for side c:

`\implies (a)/(\sin A)=(c)/(\sin C)`

`\implies (14)/(\sin 110^(\circ))=(c)/(\sin 32.8367482...^(\circ))`

`\implies c=(14\sin 32.8367482...^(\circ))/(\sin 110^(\circ))`

`\implies c=8.07866414...`

`\implies c=8.1`

`\hrulefill`

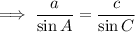
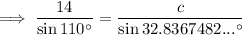
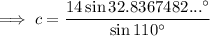
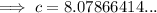
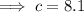
Question 4

Given values:

• b = 21
• c = 13
• B = 110°

Substitute the given values into the formula and solve for angle C:

`\implies (b)/(\sin B)=(c)/(\sin C)`

`\implies (21)/(\sin 110^(\circ))=(13)/(\sin C)`

`\implies 21 \sin C=13\sin 110^(\circ)`

`\implies \sin C=(13\sin 110^(\circ))/(21)`

`\implies C=\sin^(-1)\left((13\sin 110^(\circ))/(21)\right)`

`\implies C=35.5712205...^(\circ)`

`\implies C=35.6^(\circ)`

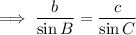
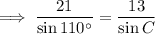
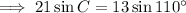
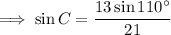
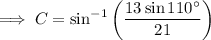
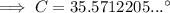
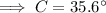
As the interior angles of a triangle sum to 180°:

`\implies A+B+C=180^(\circ)`

`\implies A=180^(\circ)-B-C`

`\implies A=180^(\circ)-110^(\circ)-35.5712205...^(\circ)`

`\implies A=34.4287794...^(\circ)`

`\implies A=34.4^(\circ)`

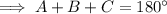
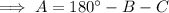
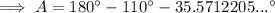
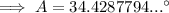
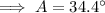
Finally, substitute the values of b, B, and A into the Law of Sines formula and solve for side a:

`\implies (a)/(\sin A)=(b)/(\sin B)`

`\implies (a)/(\sin 34.4287794...^(\circ))=(21)/(\sin 110^(\circ))`

`\implies a=(21\sin 34.4287794...^(\circ))/(\sin 110^(\circ))`

`\implies a=12.6349923...`

`\implies a=12.6`