Question

NO LINKS!! URGENT HELP PLEASE!!!

Solve ΔABC using the Law of Cosines

1. B= 36°, c = 19, a = 11

2. a = 21, b = 26, c = 17

Answer 1

1) A = 32.6°, C = 111.4°, b = 12.0

2) A = 53.6°, B = 85.7°, C = 40.7°

Explanation:

Question 1

Given values of triangle ABC:

• B= 36°
• c = 19
• a = 11

First, find the measure of side b using the Law of Cosines for finding sides.

`\boxed{\begin{minipage}{6 cm}\underline{Law of Cosines (for finding sides)} \\\\$c^2=a^2+b^2-2ab \cos (C)$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}`

As the given angle is B, change C for B in the formula and swap b and c:

`b^2=a^2+c^2-2ac\cos(B)`

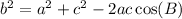
Substitute the given values and solve for b:

`\implies b^2=11^2+19^2-2(11)(19)\cos(36^(\circ))`

`\implies b^2=482-418\cos(36^(\circ))`

`\implies b=\sqrt{482-418\cos(36^(\circ))}`

`\implies b=11.9929519...`

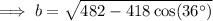
Now we have the measures of all three sides of the triangle, we can use the Law of Cosines for finding angles to find the measures of angles A and C.

`\boxed{\begin{minipage}{7.6 cm}\underline{Law of Cosines (for finding angles)} \\\\$\cos(C)=(a^2+b^2-c^2)/(2ab)$\\\\\\where:\\ \phantom{ww}$\bullet$ $C$ is the angle. \\ \phantom{ww}$\bullet$ $a$ and $b$ are the sides adjacent the angle. \\ \phantom{ww}$\bullet$ $c$ is the side opposite the angle.\\\end{minipage}}`

To find the measure of angle A, swap a and c in the formula, and change C for A:

`\implies \cos(A)=(c^2+b^2-a^2)/(2cb)`

`\implies \cos(A)=(19^2+(11.9929519...)^2-11^2)/(2(19)(11.9929519...))`

`\implies \cos(A)=0.842229094...`

`\implies A=\cos^(-1)(0.842229094...)`

`\implies A=32.6237394...^(\circ)`

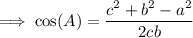
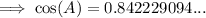
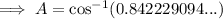
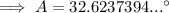
To find the measure of angle C, substitute the values of a, b and c into the formula:

`\implies \cos(C)=(a^2+b^2-c^2)/(2ab)`

`\implies \cos(C)=(11^2+(11.9929519...)^2-19^2)/(2(11)(11.9929519...))`

`\implies \cos(C)=-0.364490987...`

`\implies C=\cos^(-1)(-0.364490987...)`

`\implies C=111.376260...^(\circ)`

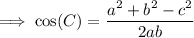
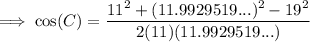
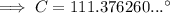
Therefore, the remaining side and angles for triangle ABC are:

• b = 12.0
• A = 32.6°
• C = 111.4°

`\hrulefill`

Question 2

To solve for the remaining angles of the triangle ABC given its side lengths, use the Law of Cosines for finding angles.

`\boxed{\begin{minipage}{7.6 cm}\underline{Law of Cosines (for finding angles)} \\\\$\cos(C)=(a^2+b^2-c^2)/(2ab)$\\\\\\where:\\ \phantom{ww}$\bullet$ $C$ is the angle. \\ \phantom{ww}$\bullet$ $a$ and $b$ are the sides adjacent the angle. \\ \phantom{ww}$\bullet$ $c$ is the side opposite the angle.\\\end{minipage}}`

Given sides of triangle ABC:

• a = 21
• b = 26
• c = 17

Substitute the values of a, b and c into the Law of Cosines formula and solve for angle C:

`\implies \cos(C)=(a^2+b^2-c^2)/(2ab)`

`\implies \cos(C)=(21^2+26^2-17^2)/(2(21)(26))`

`\implies \cos(C)=(828)/(1092)`

`\implies C=\cos^(-1)\left((828)/(1092)\right)`

`\implies C=40.690560...^(\circ)`

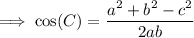
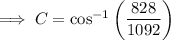
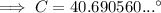
To find the measure of angle B, swap b and c in the formula, and change C for B:

`\implies \cos(B)=(a^2+c^2-b^2)/(2ac)`

`\implies \cos(B)=(21^2+17^2-26^2)/(2(21)(17))`

`\implies \cos(B)=(54)/(714)`

`\implies B=\cos^(-1)\left((54)/(714)\right)`

`\implies B=85.6625640...^(\circ)`

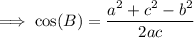
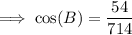
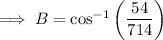
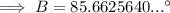
To find the measure of angle A, swap a and c in the formula, and change C for A:

`\implies \cos(A)=(c^2+b^2-a^2)/(2cb)`

`\implies \cos(A)=(17^2+26^2-21^2)/(2(17)(26))`

`\implies \cos(A)=(524)/(884)`

`\implies A=\cos^(-1)\left((524)/(884)\right)`

`\implies A=53.6468753...^(\circ)`

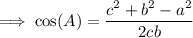
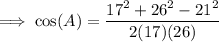
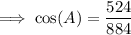
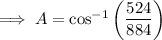
Therefore, the measures of the angles of triangle ABC with sides a = 21, b = 26 and c = 17 are:

• A = 53.6°
• B = 85.7°
• C = 40.7°