a) The value of
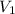 = 2.05 m/s and
= 2.05 m/s and
 = 1.45 m/s.
= 1.45 m/s.
b) The collision is not elastic.
We can use conservation of momentum and conservation of energy to solve this problem.
(a) Calculation of
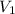 and
and
 :
:
Conservation of momentum in the x-direction:
5 kg × 2 m/s = 5 kg
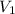 cos(30°) + 5 kg
cos(30°) + 5 kg
 cos(60°)
cos(60°)
Simplifying this equation, we get:
2 =
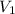 cos(30°) +
cos(30°) +
 cos(60°)
cos(60°)
Conservation of momentum in the y-direction:
0 = 5 kg
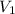 sin(30°) - 5 kg
sin(30°) - 5 kg
 sin(60°)
sin(60°)
Simplifying this equation, we get:
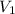 sin(30°) =
sin(30°) =
 sin(60°)
sin(60°)
Squaring both sides, we get:
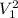 sin^2(30°) =
sin^2(30°) =
 sin^2(60°)
sin^2(60°)
Substituting sin(30°) = 0.5 and sin(60°) = 0.866, we get:
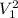 (0.25) =
(0.25) =
 (0.75)
(0.75)
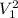 = 3
= 3

Substituting this relation into the equation for conservation of momentum in the x-direction, we get:
2 =
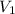 cos(30°) +
cos(30°) +
 cos(60°)
cos(60°)
2 = (

 )) / 2 +
)) / 2 +
 / 2
/ 2
4 = v2
 +
+

 = 1.45 m/s
= 1.45 m/s
Substituting this value of
 into the equation for
into the equation for
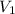 we get:
we get:
2 =
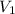 cos(30°) +
cos(30°) +
 cos(60°)
cos(60°)
2 =
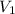
 ) / 2 + (1.45 m/s) / 2
) / 2 + (1.45 m/s) / 2
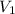 = 2.05 m/s
= 2.05 m/s
Therefore,
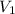 = 2.05 m/s and
= 2.05 m/s and
 = 1.45 m/s.
= 1.45 m/s.
(b) Calculation of whether the collision is elastic:
To determine if the collision is elastic, we can use the coefficient of restitution (e):
e = (
 f - v1f) / (
f - v1f) / (
 i - v1i)
i - v1i)
where
 i and
i and
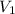 i are the initial velocities of the two pucks, and v2f and
i are the initial velocities of the two pucks, and v2f and
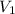 f are their final velocities.
f are their final velocities.
In this case, the initial velocity of the second puck is 0, so the coefficient of restitution simplifies to:
e =
 f /
f /
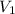 i
i
Substituting the values of
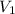 i and
i and
 f, we get:
f, we get:
e = 1.45 m/s / 2 m/s = 0.725
Since the coefficient of restitution is less than 1, the collision is not elastic. Some kinetic energy is lost during the collision, possibly due to deformation of the pucks or friction between them and the ice.