Question

NO LINKS!! URGENT HELP PLEASE!!!!

Measuring a Pond: A surveyor is measuring the width of a pond. The transit is setup at point C and forms an angle of 37° from point A to point B. The distance from point C to point A is 54 feet and the distance from point C to point B is 72 feet. How wide is the pond from point A to point B?

Answer 1

43.47 feet (2 d.p.)

Explanation:

Points A, B and C form a triangle.

We have been given sides a and b, and their included angle C.

The distance between points A and B is side c of triangle ABC.

Therefore, we can solve this problem using the Law of Cosines, which relates the lengths of the sides of a triangle to the cosine of one of its angles.

`\boxed{\begin{minipage}{6 cm}\underline{Law of Cosines (for finding sides)} \\\\$c^2=a^2+b^2-2ab \cos (C)$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}`

Given values:

• a = side CB = 72 ft
• b = side CA = 54 ft
• C = angle ACB = 37°

Substitute the given values into the Law of Cosines formula and solve for side c:

`\implies c^2=72^2+54^2-2(72)(54)\cos(37^(\circ))`

`\implies c^2=8100-7776\cos(37^(\circ))`

`\implies c=\sqrt{8100-7776\cos(37^(\circ))}`

`\implies c=43.4719481...`

`\implies c=43.47\; \sf ft\;(2\; d.p.)`

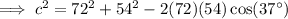
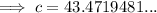
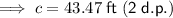
Therefore, the width of the pond from point A to point B is 43.47 feet, to two decimal places.