Question

Task 4:

A carnival attraction tests your strength by how far in the air

you can drive a weight with a hammer. If the weight

reaches 15 feet you win a prize! The equation

h = -1612 + 317 + 2 gives the height h of the weight t seconds

after you hit it.

A: How long is the weight moving?

B: What was the weight's maximum height?

C: Did you win a prize? How do you know?

Answer 1

B i think i am sorry if it is not right but i am pretty sure i am right tho

Answer 2

a. The amount of time for which the weight stayed in the air is 2 seconds.

b. The weight’s maximum height is approximately 17.0 feet.

c. Yes, I won a prize because the weight exceeded the minimum height of 15 feet.

Based on the information provided, we can logically deduce that the height (h), in feet, of this weight is related to time (in seconds) by the following quadratic function:

`h = -16t^2 +31t+2`

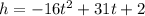
Part a.

In order to determine the amount of time for which the weight stayed in the air, we would equate the height function to zero and solve for the greater value of t as follows;

`0 = -16t^2 +31t+2\\\\16t^2-31t-2=0\\\\t = (-b\; \pm \;√(b^2 - 4ac))/(2a)\\\\t = (-(-31)\; \pm \;√((-31)^2 - 4(16)(-2)))/(2(16))\\\\t = (31\; \pm \;√(961 + 128))/(32)\\\\t = (31\; \pm \;√(1089))/(32)\\\\t = (31\; \pm \;33)/(32)`

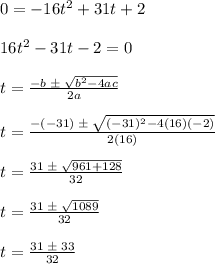
t = ±2 seconds.

Since time must be a positive number, the value of t is 2 seconds.

Part b.

Next, we would determine the maximum height of this weight by using the axis of symmetry formula to determine the time (t) it takes;

t = -b/(2a)

t = -31/(-16 × 2)

t = 31/32

t = 0.9688

By substituting the time (t) above into the height function, the weight’s maximum height is given by;

`h = -16t^2+ 31t + 2\\\\h = -16(0.9688)^2+ 31(0.9688) + 2`

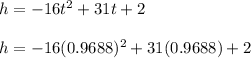
h = 17.02 ≈ 17.0 feet.

Part c.

Since my weight reached a maximum height of approximately 17 feet, it implies that I won a prize because the weight exceeded the minimum height of 15 feet.

Complete Question:

A carnival attraction tests your strength by how far in the air you can drive a weight with a hammer. If the weight reaches 15 feet, you win a prize. The equation
`h = -16t^2+ 31t + 2` gives the height, in feet, and time, in seconds of the weight after it is hit.

a. How long is the weight in the air?

b. What was the weight’s maximum height?

c. Did you win a prize? Why or why not?