Question

A child that is 4.5 feet tall is standing in the playground. The sun is shining and the child casts a shadow 10 feet long. At the same time, a tree casts a shadow that is 24 feet long. How tall is the tree?

Answer 1

10.8 feet

Explanation:

The problem involves using proportions to find the height of the tree, based on the height of the child and the lengths of the two shadows.

To set up the proportion, first recognize that the ratio of the height of the child to the length of their shadow is the same as the ratio of the height of the tree to the length of its shadow.

This can be written mathematically as:

`\boxed{\sf (height\;of\;the\;child)/(child\;shadow\;length)=(height\;of\;the\;tree)/(tree\;shadow\;length)}`

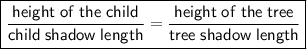
Let the height of the tree be x.

Given the height of the child is 4.5 feet, the length of the child's shadow is 10 feet, and the length of the tree's shadow is 24 feet:

`\begin{aligned}\sf (height\;of\;the\;child)/(child\;shadow\;length)&=\sf (height\;of\;the\;tree)/(tree\;shadow\;length)\\\\(4.5)/(10)&=(x)/(24)\end{aligned}`

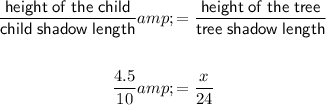
To solve for x, multiply both sides of the equation by 24 and simplify:

`24 \cdot (4.5)/(10)=24 \cdot (x)/(24)`

`(108)/(10)=x`

`10.8=x`

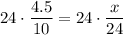
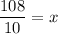
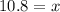
Therefore, the height of the tree is 10.8 feet.

Answer 2

• The tree is 10.8 feet

---------------------------

The formed triangles are similar right triangles.

They have equal ratios of corresponding sides.

Let the tree is t feet high, then we have ratios:

• t/4.5 = 24/10

Solve it for t:

• t/4.5 = 2.4
• t = 4.5*2.4
• t = 10.8