Question

Find two positive numbers whose squares have a sum of 74 and a difference of 24.

Answer 1

Explanation:

Given,

Two positive number whose squares have a sum of 74 and a difference of 24

To Find:

The two positive number.

Explanation

Let the two positive numbers be x and y.

Then according to the question, we have two equations:

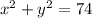`x^2 + y^2 = 74` (equation 1)

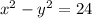`x^2 - y^2 = 24` (equation 2)

Now, use equation 2 to solve for one of the variables in terms of the other.

Adding
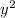`y^2` to both sides gives:

`x^2 = y^2 + 24`

Taking the square root of both sides gives:

`x = √((y^2 + 24))`

Now substitute this expression for x into equation 1 and solve for y:

`(y^2 + 24) + y^2 = 74`

`2y^2 + 24 = 74`

`2y^2 = 50`

`y^2 = 25`

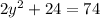
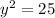
`y = 5` (since we're looking for a positive number)

Now we can use the expression we found for x to get:

`x = √((y^2 + 24)) = √(25 + 24) = √(49) = 7`

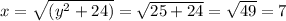
So the two positive numbers are x = 7 and y = 5.

Therefore, the solution is x = 7 and y = 5.

Answer 2

7 and 5

Explanation:

Let x and y be the two unknown positive numbers.

Set up a system of equations using the defined variables and the given information:

`\begin{cases}x^2 + y^2 = 74\\x^2 - y^2 = 24 \end{cases}`

Solve the system of equations by the method of elimination.

Add the two equations to eliminate the terms in y:

`\begin{array}{crcccc}&x^2&+&y^2&=&74\\\vphantom{\frac12}+&x^2&-&y^2&=&24\\\cline{2-6}\vphantom{\frac12}&2x^2&&&=&98\end{array}`

Solve for x:

`\begin{aligned}2x^2&=98\\2x^2 / 2&=98 / 2\\x^2&=49\\√(x^2)&=√(49)\\x&=\pm7\end{aligned}`

As x is positive, x = 7 only.

To find the value of y, substitute x = 7 into one of the equations:

`\begin{aligned}x^2+y^2&=74\\(7)^2+y^2&=74\\49+y^2&=74\\49+y^2-49&=74-49\\y^2&=25\\√(y^2)&=√(25)\\y&=\pm 5\end{aligned}`

As y is positive, y = 5 only.

Therefore, the two positive numbers whose squares have a sum of 74 and a difference of 24 are 7 and 5.