Question

Solve by completing the square.

j² + 14j + 5 = 0
Write your answers as integers, proper or improper fractions in simplest form, or decimals
rounded to the nearest hundredth.
Submit
or j =
=

Answer 1

`j = 7 \pm √(44)`

Explanation:

First, move the constant term to the other side of the equation.

`j\² + 14j + 5 = 0`

`j\² + 14j = -5`

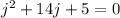
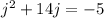
Next, add the coefficient of the first degree j term divided by 2, then squared to both sides.

`j^2 + 14j + (14/2)^2 = -5 + (14/2)^2`

`j^2 + 14j + (7)^2 = -5 + (7)^2`

`j^2 + 14j + 49 = -5 + 49`

`j^2 + 14j + 49 = 44`

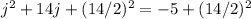
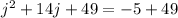
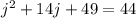
Now, we can factor the left side as a square.

`(j+7)(j+7) = 44`

`(j+7)^2 = 44`

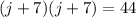
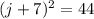
Finally, we can take the square root of both sides to solve for j.

`√((j+7)^2) = \sqrt{44`

`j+7=\pm√(44)`

`\boxed{j = 7 \pm √(44)}`

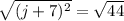
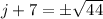
Note that there are two solutions, as
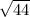`\sqrt{44` could be positive OR negative because of the even root property:

if
`x^2 = a^2`,

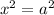then
`x = \pm a`

because both
`(+a)^2` and
`(-a)^2` equal
`a^2`.