Question

Use the triangle below to determine which of the following statements are true a. (Sin A)^2 + ( Cos A)^2=1.

Answer 1

The trigonometric identity
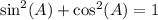`\( \sin^2(A) + \cos^2(A) = 1 \)` is true for any angle A in a right-angled triangle. Therefore, the statement
`\((\sin A)^2 + (\cos A)^2 = 1\)` is also true. This expression represents the Pythagorean Identity.

Explanation:

The trigonometric identity
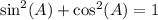`\( \sin^2(A) + \cos^2(A) = 1 \)` is a fundamental relationship in trigonometry known as the Pythagorean Identity. It stems from the Pythagorean Theorem applied to the unit circle. In a right-angled triangle within the unit circle, the length of the hypotenuse is 1, and the coordinates of a point on the circle can be expressed as
`\((\cos A, \sin A)\)`, where A is the angle formed with the positive x-axis.

The Pythagorean Identity asserts that the square of the sine of an angle plus the square of the cosine of that angle equals 1. This holds true for all angles, not just those in right-angled triangles. Essentially, it showcases the inherent relationship between the sine and cosine functions and highlights their complementary nature. As one function increases, the other decreases in such a way that their squares always sum to 1. This identity is not only a cornerstone of trigonometry but also finds extensive applications in physics, engineering, and various scientific disciplines where the understanding of periodic functions is crucial.

Answer 2

Answer 4

Explanation: