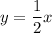Question

ABCD is a rhombus. A has coordinates (2,- 4) and C (-2, 4). Find the equation of the diagonal

BD.

Answer 1

`y =(1)/(2)x`

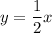
Explanation:

General slope-intercept form of a straight line is
y = mx + b
where m = slope, b = y-intercept

The diagonals of a rhombus bisect each other at 90°

The equation of diagonal AC can be found as follows

Slope of AC =
`(4 - (-4))/(-2 - 2) = (8)/(-4) = - 2\\`

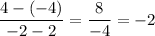
Therefore the diagonal AC has the equation
y = -2x + b

where b is the y intercept

We can find b by plugging in (-2, 4) into the above equation:
4 = -2(-2) + b

4 = b + b

b = 0

So the equation of the diagonal is y = -2x

This passes through the origin (0,0)

Since A and C are equidistant from the origin, the origin is the midpoint of the diagonal AC

Since the other diagonal BD has to bisect this diagonal at 90°, it too has to pass through the midpoint (0, 0)

The slope of a line perpendicular to y = mx + b is -1/m

Therefore the slope of the perpendicular line to y = -2x is - (1/-2) = 1/2 and the y-intercept is 0 since it passes through the origin

Therefore the equation of diagonal BD is

`y =(1)/(2)x`