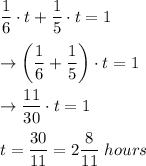Question

Shawna can paint a fence in 6 hours. Kevin can paint the same fence in 5 hours. How long will it take them working together? Which of the following equations could be used to solve this problem? ​

Answer 1

Explanation:

Answer 2

Second Option

`\left((1)/(6) \right)\cdot t + \left((1)/(5) \right)\cdot t = 1`

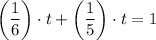
Explanation:

Shawna can paint the fence in 6 hours. So her rate of work is 1/6 of the fence in one hour

Kevin can paint the same fence in 5 hours so his rate of work is 1/5

Working together their combined rate
= 1/6 + 1/5

Let the time taken for both of them working together to paint the entire fence be t hours

In t hours
amount of work done by each = rate x time
For Shawna:

`(1)/(6) \cdot t`

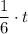
For Kevin:

`(1)/(5) \cdot t`

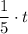
The total work done must add up to the whole fence which can be represented as 1

Therefore the equation for computing the time taken for both of them to work together is given by

`(1)/(6) \cdot t + (1)/(5) \cdot t = 1`

This is the second option

`-------------------------------------------`

As an aside
While you have not been asked to solve the problem, we can still do it as an exercise:

`(1)/(6) \cdot t + (1)/(5) \cdot t = 1\\\\\rightarrow \left((1)/(6) + (1)/(5) \right) \cdot t = 1\\\\\rightarrow (11)/(30) \cdot t = 1\\\\t = (30)/(11) = 2 (8)/(11) \;hours`