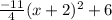Question

NO LINKS!! URGENT HELP PLEASE!!!

Find the equation of a parabola with a vertex at (-2, 6) and that passes through the (-4, -5)

Answer 1

`(-11)/(4) (x + 2)^2 + 6.`

Explanation:

As we know that

The standard equation of a parabola with vertex at point (h,k) is given by:

`y = a(x-h)^2 + k`

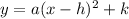
where (h,k) is the vertex

and "a" is a coefficient that determines the direction and shape of the parabola.

We know that the vertex of our parabola is (-2, 6),

so we can substitute those values into the equation to get:

`y = a(x + 2)^2 + 6`

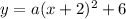
Now finding a.

Since the parabola passes through point (-4, -5). Substituting these coordinates into the equation, we get:

-5 = a(-4 + 2)^2 + 6

-5 =a(-2)^2+6

-5=4a +6

-5-6=4a

4a=-11

a =- 11/4

Substituting the value of an equation second, we get

`(-11)/(4) (x + 2)^2 + 6.`

Therefore, the equation of the parabola with a vertex at (-2, 6) and passing through (-4, -5) is y =

`(-11)/(4) (x + 2)^2 + 6`

Answer 2

`y=-(11)/(4)(x+2)^2+6`

Explanation:

The vertex form of a parabola is:

`\boxed{y=a(x-h)^2+k}`

where:

• (h, k) is the vertex.
• "a" is the leading coefficient.

Given the vertex is at (-2, 6), substitute h = -2 and k = 6 into the equation:

`y=a(x-(-2))^2+6`

`y=a(x+2)^2+6`

To find the value of a, substitute the point (-4, -5) into the equation and solve for a:

`\begin{aligned}-5&=a(-4+2)^2+6\\-5&=a(-2)^2+6\\-5&=4a+6\\-5-6&=4a+6-6\\-11&=4a\\(-11)/(4)&=(4a)/(4)\\-(11)/(4)&=a\\a&=-(11)/(4)\end{aligned}`

Substitute the found value of a back into the equation:

`y=-(11)/(4)(x+2)^2+6`

Therefore, the equation of a parabola with a vertex at (-2, 6) and that passes through the point (-4, -5) is:

`\boxed{y=-(11)/(4)(x+2)^2+6}`