Question

NO LINKS!! URGENT HELP PLEASE!!!!

y = 3*2^x - 6

Name the "family" and state the parent function.

Answer 1

Exponential function family with base 2.

`\textsf{Parent function:} \quad y=2^x`

Explanation:

The given equation is in the form of an exponential function with a vertical stretch and vertical shift.

The standard form of this type of exponential function is:

`y=ab^x+c`

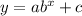
where:

• a is the vertical stretch factor.
• b is the base (growth/decay factor) in decimal form.
• c is the vertical shift.
• y = c is the equation of the horizontal asymptote.

If |a| > 1 then it is a vertical stretch, and if 0 < |a| < 1 it is a vertical "compression".

The parent function of this type of exponential function is y = bˣ, where b is the base.

Given function:

`y=3 \cdot 2^x-6`

Therefore, the parent function of the given function is:

`\boxed{f(x)=2^x}`

The given function is a vertical stretch by a factor of 3, followed by a vertical shift downwards by 6 units, from the parent exponential function with base 2.

Hence, the family of functions that this equation belongs to is the exponential function family with base 2, and the parent function is
`y = 2^x`.

Answer 2

Family: exponential functions

Explanation:

The given function is:

`y = 3*2^x - 6`

It is in the form of exponential function:

`y = a*b^x + c`

where "a", "b", and "c" are constants.

The parent function of an exponential function is:

`y = b^x`

where "b" is the base of the exponential function. In this case, the parent function would be:

The given function is a member of the family of exponential functions with base 2 and with a vertical shift of -6 units and a vertical stretch by a factor of 3.