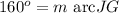Question

What is the measure of JG

Answer 1

measure of arc JG = 160 degrees

Explanation:

Main Concept: Intersecting chords

Chords are line segments with ends points that are both on the edge of the circle. Intersecting chords are a pair of chords on the same circle that intersect.

In an extreme example, the chords may intersect at one of the end points, making the intersecting chords an inscribed angle.

Because Intersecting chords intersect, if the line segments are extended into lines, the lines form two pairs of vertical angles. Vertical angles are congruent. Given one vertical angle pair, they will contain two arcs (in the extreme case, the arc will have a measure of zero).

The measure of each of the vertical angles is the average of the two contained arcs.

This problem

For this problem, FG and HJ are chords of the same circle, and they intersect.

If we call the intersection P, angle GPJ is given with a measure of 100 degrees.

Angle GPJ and Angle FPJ form a vertical angle pair, so they are congruent, because vertical angles are congruent.

The measure of each of the vertical angles is the average of the two contained arcs.

The two arcs that this vertical angle pair contain are the arc JG and arc FH.

The measure of arc FH is given as 40 degrees.

Substitute these known quantities into the equation describing the relationship between one of the vertical angles and the contained arcs.

`m \angle GPJ=(1)/(2)(m ~\text{arc}JG + m ~\text{arc}FH)`

`(100^o)=(1)/(2)(m ~\text{arc}JG + (40^o))`

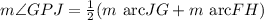
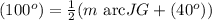
Multiply both sides by 2...

`200^o=m ~\text{arc}JG + 40^o`

Subtract 40 degrees from both sides...

`160^o=m ~\text{arc}JG`