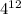Ordering the expressions from least to greatest: 1.
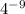 , 2.
, 2.
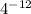 , 3.
, 3.
 , 4.
, 4.
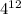
Let's simplify each expression to compare them:
1.
 can be simplified by multiplying the exponents:
can be simplified by multiplying the exponents:
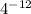 .
.
2.
 can be simplified by subtracting the exponents in the denominator from the exponents in the numerator:
can be simplified by subtracting the exponents in the denominator from the exponents in the numerator:
 .
.
3.
 can be simplified by adding the exponents:
can be simplified by adding the exponents:
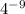 .
.
4.
 can be simplified by changing the reciprocal and sign of the exponent:
can be simplified by changing the reciprocal and sign of the exponent:
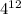 .
.
Now, let's order them from least to greatest:
1.
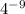
2.
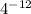
3.

4.