Answer:
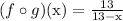
Domain:
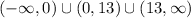
=================================================
Step-by-step explanation:
Let's find the function composition.
The notation
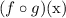 is the same as
is the same as
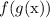
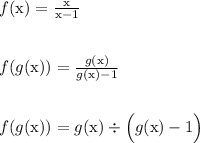
Then,
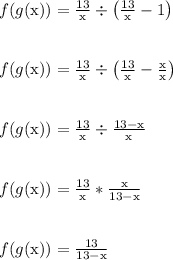
-----------------
Now let's find the domain.
If we plugged x = 0 into g(x), then we get a division by zero error.
This means we must exclude this value from the domain.
For similar reasoning, we must exclude x = 13 because we get a division by zero error in

We could have any other real number to be plugged in for x.
Here's what the domain looks like in interval notation.
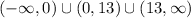
We effectively poke holes at 0 and 13 on the number line.