Answer:
n = 20/3
Explanation:
Theory about the discriminant, and how solutions are acquired via the quadratic formula
One variable quadratic equations in the form
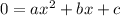 have exactly one solution when the discriminant
have exactly one solution when the discriminant
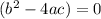 .
.
This is because for quadratic equations of the original form, the two solutions are given by the quadratic formula:

which is equivalent to
 .
.
The
 is the axis of symmetry, and the
is the axis of symmetry, and the
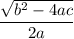 part is how much the solutions deviate from the axis of symmetry. If the deviation is zero, then the two solutions are both ON the axis of symmetry, and are the same number, giving exactly one solution.
part is how much the solutions deviate from the axis of symmetry. If the deviation is zero, then the two solutions are both ON the axis of symmetry, and are the same number, giving exactly one solution.
Addressing the given equation
Putting it into standard form
Given the given equation...
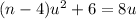
subtract 8u from both sides to obtain an equation that looks like the standard form equal to zero...
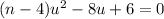
The variable here is "u" instead of "x", so the solutions to this equation would be
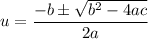 , where
, where
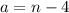 ,
,
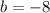 , and
, and
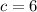 .
.
Identifying the discriminant
The discriminant then, with values of a, b, and c, substituted, becomes:
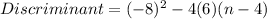
If we want the discriminant to equal zero (so that there is exactly one solution for "u"), substitute zero on the left side of the equation, and solve for n.
Solving for n
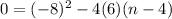
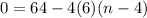

Add -24(n-4) to both sides...
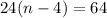
Divide both sides by 24...

Reduce the right hand side...
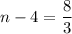
Add 4 to both sides...

Find a common denominator...
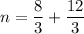
Find a common denominator...
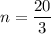
So, if
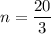 , then the equation
, then the equation
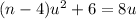 has exactly one solution. Furthermore, this is the only value of "n" for which the equation has exactly one solution, because it is the only value of "n" for which the discriminant is zero.
has exactly one solution. Furthermore, this is the only value of "n" for which the equation has exactly one solution, because it is the only value of "n" for which the discriminant is zero.