Question

Write an equation for the circle graphed below.

-4
-2
6
4
2
-2
-4
-6
2

Answer 1

`\left(x\:+\:1\right)^2\:+\:y^2=25`

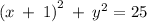
Explanation:

The equation of a circle with radius r and center at (a, b) is given by
(x - a)² + (y - b)² = r²

Let's first find the radius

The circle intersects the x axis at two points (-6, 0) and (4, 0)

The diameter is therefore the absolute difference between the x values:
|-6 - 4| same as |4 - (-6)| = 10

The radius r = 5 (half of diameter)

Now, let's find the center point of the circle. This will lie midway between (-6, 0) and (4, 0)

Midpoint (xm, ym) between two points(x1, y) and (x2, y2) :
xm = (x1 + x2)/2 = (-6 + 4)/2 = -1
ym = (y1 + y2)/2 = (0 + 0)/2 = 0

So the center (a, b) = (-1, 0) with a = -1, b = 0

The equation of the circle therefore is
(x - a)² + (y - b)² = r²
( x - (-1) )² + (y - 0)² = 25

(x + 1)² + y² = 25

To find a and b take any point (x, y) and plug these