Answer:
Vertical Compression by factor of 1/4
Explanation:
Two methods:
Method 1. Transformations
Method 2. Algebraic input-output tables
Method 1. Transformations
The Main concept of this question is about Transformations of functions -- specifically, multiplying on the outside by a positive number less than 1.
The transformation that occurs when multiplying a function by a positive number on the outside of the function is a vertical stretch or compression.
Positive numbers larger than 1 will stretch it vertically, whereas positive numbers smaller than 1 will compress it vertically.
Therefore, multiplying by 1/4 on the outside, a positive number less than 1, will vertically compress the function down to one-fourth the size.
This means that for g(x), all points on the original function f will have their heights reduced to 1/4 their original height (or depth) -- making all points on g(x) 1/4 their previous distance from the x-axis on the "f" function.
Method 2. Algebraic input-output tables
Observe on the graph three points on the function f:
- (0,0), (1,4) and (3,0) --- points on the function "f"
- In function notation, this means
 ,
,
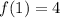 , and
, and
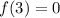
Using the equation relating f and g,
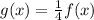 , we can find how those points would look like on the new function g(x).
, we can find how those points would look like on the new function g(x).
For

![g(0)=(1)/(4)[f(0)]\\g(0)=(1)/(4)[0]\\g(0)=0](https://img.qammunity.org/2024/formulas/mathematics/high-school/ah4s9yqxjmobaissrjppmhn9x379dqt2n7.png)
For
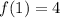
![g(1)=(1)/(4)[f(1)]\\g(1)=(1)/(4)[4]\\g(1)=1](https://img.qammunity.org/2024/formulas/mathematics/high-school/549c8q42vh0tguxr58rw0oxeen0f9n151t.png)
For
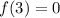
![g(3)=(1)/(4)[f(3)]\\g(3)=(1)/(4)[0]\\g(3)=0](https://img.qammunity.org/2024/formulas/mathematics/high-school/x23vdh2vhxkmtxsafvwuv7fzqj6wek9ugx.png)
These known points should correctly identify the graph from the possible choices.