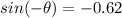Question

Use the even and odd properties of the following functions to answer the questions:

a) If sec⁡θ=-3.1,then sec⁡(-θ)=?

b)If sin⁡θ=0.62,then sin⁡(-θ)=?

Answer 1

`sec(-\theta)=-3.1`

`sin(-\theta)=-0.62`

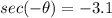
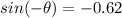
Explanation:

Part a.

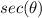`sec(\theta)` is related to
`cos(\theta)` through a reciprocal relationship
`sec(\theta)=(1)/(cos(\theta))`.

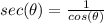Since
`cos(\theta)` is an even function (reflecting left-right across the y-axis doesn't change the graph), then
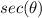`sec(\theta)` is also an even function.

For any input in the domain, even functions produce the same output if the opposite of the input is used. In other words, if "f" is an even function, for all x in the domain of f,
`f(x)=f(-x)`.

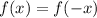Thus, for the secant function, if a mystery value "x" is used as an input, and -3.1 is obtained as an output, then if the opposite of x, or -x, is input into the secant function, the output will also be -3.1.

`sec(-\theta)=-3.1`

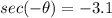
Part b.

The
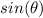`sin(\theta)` function does not reflect left-right across the y-axis to produce the same graph, so the sine function is not even.

However, the sine function can be rotated 180 degree about the origin, sometimes thought of as reflecting through the origin, to produce the same graph. Visually, this is an "odd" function.

For any input in the domain, if the opposite of the input is used, odd functions produce the opposite of the original output. In other words, if "g" is an odd function, for all x in the domain of g,
`-g(x)=g(-x)`.

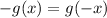Thus, for the sine function, if a mystery value "x" is used as an input, and 0.62 is obtained as an output, then if the opposite of x, or -x, is input into the sine function, the output will be the opposite of 0.62, meaning -0.62.

`sin(-\theta)=-0.62`