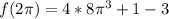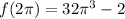Answer:
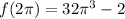
Explanation:
Main steps:
Step 1: Use integration to find a general equation for f
Step 2: Find the value of the constant of integration
Step 3: Find the value of f for the given input
Step 1: Use integration to find a general equation for f
If
 , then
, then
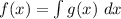
![f(x) = \int [12x^2 - sin(x)] ~dx](https://img.qammunity.org/2024/formulas/mathematics/college/dl9eb1zs5w6wyg3th5sb8qsep9f1dmic2k.png)
Integration of a difference is the difference of the integrals
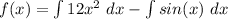
Scalar rule
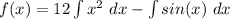
Apply the Power rule & integral relationship between sine and cosine:
- Power Rule:
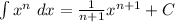
- sine-cosine integral relationship:
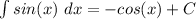
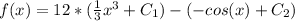
Simplifying
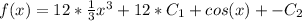
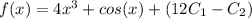
Ultimately, all of the constant of integration terms at the end can combine into one single unknown constant of integration:
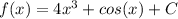
Step 2: Find the value of the constant of integration
Now, according to the problem,
 , so we can substitute those x,y values into the equation and solve for the value of the constant of integration:
, so we can substitute those x,y values into the equation and solve for the value of the constant of integration:
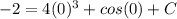

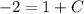
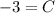
Knowing the constant of integration, we now know the full equation for the function f:
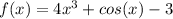
Step 3: Find the value of f for the given input
So, to find
 , use 2 pi as the input, and simplify:
, use 2 pi as the input, and simplify: