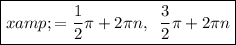Find all solutions of the equation in radians. sin(2x)sin(x)+cos(x)=0

Question

asked Mar 25, 2024 113k views

1 Answer

Derek Brown · Answer 1 · 2024-03-28T23:26:25+0000

Answer:

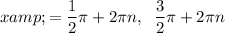
$x&=(1)/(2)\pi +2\pi n,\;\; (3)/(2)\pi + 2 \pi n$

Explanation:

Given equation:

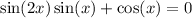
$\sin(2x)\sin(x)+\cos(x)=0$

Rewrite sin(2x) using the trigonometric identity sin(2x) = 2sin(x)cos(x):

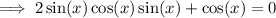
$\implies 2\sin(x)\cos(x)\sin(x)+\cos(x)=0$

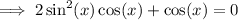
$\implies 2\sin^2(x)\cos(x)+\cos(x)=0$

Factor out cos(x):

$\implies \cos(x)\left[2\sin^2(x)+1\right]=0$

Applying the zero-product property:

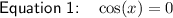
$\textsf{Equation 1:}\quad\cos(x)=0$

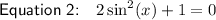
$\textsf{Equation 2:}\quad2\sin^2(x)+1=0$

Solve each part separately.

$\underline{\sf Equation \; 1}$

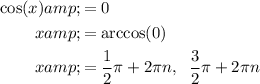
$\begin{aligned}\cos(x)&=0\\x&=\arccos(0)\\x&=(1)/(2)\pi +2\pi n,\;\; (3)/(2)\pi + 2 \pi n\end{aligned}$

$\underline{\sf Equation \; 2}$

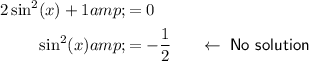
$\begin{aligned}2\sin^2(x)+1&=0\\\sin^2(x)&=-(1)/(2)\;\;\;\;\;\;\leftarrow\;\textsf{No solution}\end{aligned}$

Therefore, the solutions of the equation in radians are:

$\boxed{x&=(1)/(2)\pi +2\pi n,\;\; (3)/(2)\pi + 2 \pi n}$