Answer:
We can use the formula for finding arc length given ccx central angle and radius.(insert formula below) We then substitute 5 in for r and and 60 for x. We multiply 2 pi times 5 which gives us 10. We then reduce the fraction of 60/360 to 1/6. We multiply 10 pi by 1/6 and that gives us
10 pi/6 or 5 pi/3
Explanation:
We can use the formula

to find the arc length where r is the radius.
and x is the arc measure.
Plug it in for the numbers
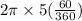
Multiply 2 pi times 5=10 pi
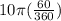
Simplify 60/360 to 1/6
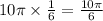
Reduce it to
