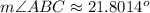Question

For the line y=2/5x+9, what will be the angle this line makes with the x-axis?

Answer 1

21.8014 degrees (to 4 decimal places)

Explanation:

The equation y=2/5x+9 forms a certain angle with the x-axis. Note that all lines parallel to y=2/5x+9 also form the same angle with the x-axis, due to Corresponding Angles (the fact that the original line has a y-intercept of 9 is irrelevant). Therefore, we could simplify this problem slightly by considering the angle that y=2/5x (a y-intercept of 0) forms with the x-axis.

To find the angle that this line makes with the x-axis, we'll need the vertex (the origin -- let's call this point "B"), and one point on each of two rays from the vertex (Let Ray #1 be the ray from the origin directly to the right; and let Ray #2 be the ray from the origin extending into Quadrant I -- up and to the right, along the equation y=2/5x).

One point on Ray #1 is (5,0) -- it is on the positive x-axis. Call this point "A"

One point on Ray #2 is (5,2) -- inputting "5" for x, the result for y is "2" Call this point "C"

• y = 2/5 * (5) = 2

To find the angle (Angle ABC), observe that the three points form a right triangle (the angle CAB is a right angle because the two lines are perpendicular).

To solve for
`\angle ABC`, recall the definition of the tangent function:

`tan(\theta)=(opposite)/(adjacent)`

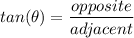
The Opposite side, side AC, is just the height (or the y-value) of point C. So, opposite = 2.

The Adjacent side, side BA, is just the x-coordinate of point A (and also point C). So adjacent = 5.

Substituting these known values into the tangent function, we get the following:

`tan(m\angle ABC)=(2)/(5)`

To solve for the measure of angle ABC, we need to apply the inverse tangent function (also known as arctangent).

`arctan(tan(m\angle ABC)=arctan((2)/(5))`

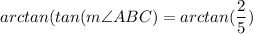
The left side simplifies because they are inverse functions:
`m\angle ABC=arctan((2)/(5))`

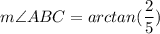
Calculating the right side of the equation (rounding to 4 decimal places):

`m\angle ABC \approx 21.8014^(o)`