Question

Jordan is tracking a recent online purchase. The shipping costs state that the item will be shipped in a 24-inch long box with a volume of 2,880 cubic inches. The width of the box is seven inches less than the height.

The volume of a rectangular prism is found using the formula V = lwh, where l is the length, w is the width, and h is the height.
Complete the equation that models the volume of the box in terms of its height, x, in inches.
Is it possible for the height of the box to be 15 inches?
also the question has 3 boxes

Answer 1

Yes

Explanation:

The only answer is height = 15 because the -8 will be rejected

Answer 2

Sure, I can help you with that.

Given:

* The box is 24 inches long.

* The width of the box is seven inches less than the height.

* The volume of the box is 2,880 cubic inches.

To solve:

* Complete the equation that models the box's volume in terms of its height, x, in inches.

* Determine if the height of the box can be 15 inches.

Solution:

Let's define the following variables:

* $h$ = the height of the box (in inches)

* $w$ = the width of the box (in inches)

* $l$ = the length of the box (in inches)

We are given that l=24 and w=h−7. We can use these values to find the volume of the box:

`V = lwh = 24(h - 7)h`

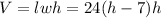
We can simplify this expression to get the following equation:

`V = 24h^2 - 168h`

To determine if the height of the box can be 15 inches, we can substitute 15 for $h$ in the equation and see if we get a positive value for the volume.

`V = 24(15)^2 - 168(15) = 2160 - 2490 = -330`

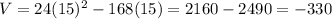
Since the volume is negative, the height of the box can't be 15 inches.

Therefore, the equation that models the box's volume in terms of its height, x, in inches is
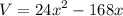`$V = 24x^2 - 168x$`. Consequently, the size of the box can't be 15 inches.