Question

Suppose that the functions f and g are defined as follows.

Answer 1

`(f)/(g)(x) = \boxed{(7)/(x\left(x-3\right))\\\\}`

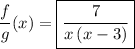
Domain of
`(f)/(g): \boxed{\:\left(-\infty \:,\:0\right)\cup \left(0,\:3\right)\cup \left(3,\:\infty \:\right)}`

Explanation:

Given

`f(x) = (7)/(x) , g(x) = x - 3`

`(f)/(g) = (f(x))/(g(x)) = (7)/(x) / x - 3\\\\= (7)/(x) * (1)/(x-3)\\\\ = (7)/(x\left(x-3\right))`

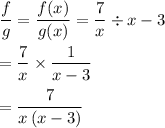
To find the domain of

`(f)/(g) = (7)/(x\left(x-3\right))`

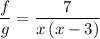
note that this function is defined everywhere in the range (- ∞, ∞) except for x = 0 and x = 3

At these two points, the function is undefined since the denominator becomes 0 and division by 0 is undefined

Therefore the domain consists of three parts expressed in inequality and interval forms

-∞ < x < 0 (-∞, 0)

0 < x < 3 (0, 3)

3 < x < ∞ (3, ∞)

Therefore the domain is obtained by combining these three intervals
- ∞ < x < 0 or 0 < x < 3 or x > 3

In interval notation with union:

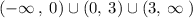`\:\left(-\infty \:,\:0\right)\cup \left(0,\:3\right)\cup \left(3,\:\infty \:\right)` ANSWER