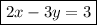Question

Find the equation of the line. The line is parallel to the graph of 2x-3y=7 and contains the point (-3, -3).

Answer 1

Explanation:

2x-3y=7 (-3,-3)

2x-7=3y

3y=2x-7

divide both sides by 3

y = 2/3x - 7/3

m1= 2/3

m1=m2 for parallel

2/3 = y-(-3)/x-(-3)

2/3= y+3/x+3

2 = y+3

– —

3 x +3

then you cross multiply

2(x+3)=3(y+3)

2x+6= 3y+9

then move everything to one side

2x-3y+6-9 =0

2x-3y-3=0

Answer 2

`\textsf{Slope-intercept form:} \quad y=(2)/(3)x-1`

`\textsf{Standard form:} \quad 2x-3y=3`

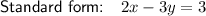
Explanation:

Parallel lines have the same slope.

Therefore, in order to find the equation of the line that is parallel to 2x - 3y = 7, we must first find the slope of this line by rearranging it in the form y = mx + b.

`\begin{aligned}2x-3y&=7\\2x-3y+3y&=7+3y\\2x&=3y+7\\2x-7&=3y+7-7\\2x-7&=3y\\3y&=2x-7\\(3y)/(3)&=(2x-7)/(3)\\y&=(2)/(3)x-(7)/(3)\end{aligned}`

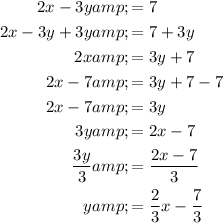
The equation y = mx + b is the slope-intercept form of a straight line, where m is the slope and b is the y-intercept. Therefore, the slope of the line is m = 2/3.

To find the equation of the line has a slope m = 2/3 and contains the point (-3, -3), we can use the point-slope form of a straight line.

`\begin{aligned}y-y_1&=m(x-x_1)\\\\\implies y-(-3)&=(2)/(3)(x-(-3))\\\\y+3&=(2)/(3)(x+3)\\\\y+3&=(2)/(3)x+2\\\\y+3-3&=(2)/(3)x+2-3\\\\y&=(2)/(3)x-1\end{aligned}`

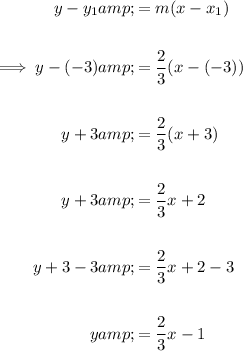
Therefore, the equation of the line that is parallel to the graph of 2x - 3y = 7 and contains the point (-3, -3) in slope-intercept form is:

`\boxed{y=(2)/(3)x-1}`

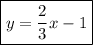
If you want the equation in standard form, rearrange the equation to Ax + By = C (where A, B and C are constants and A must be positive):

`\begin{aligned}y&=(2)/(3)x-1\\\\3 \cdot y&=3 \cdot \left((2)/(3)x-1\right)\\\\3y&=2x-3\\\\3y+3&=2x-3+3\\\\3y+3&=2x\\\\3y+3-3y&=2x-3y\\\\3&=2x-3y\\\\2x-3y&=3\end{aligned}`

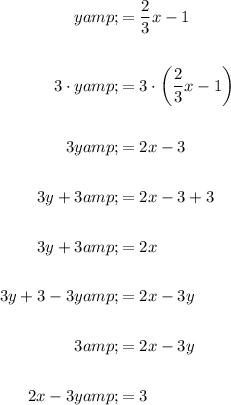
Therefore, the equation of the line that is parallel to the graph of 2x - 3y = 7 and contains the point (-3, -3) in standard form is:

`\boxed{2x-3y=3}`