Question

The height h(n) of a bouncing ball is an exponential function of the number n of bounces.

One ball is dropped and on the first bounce reaches a height of 6 feet. On the second

bounce it reaches a height of 4 feet.

PLEASE HURRY

Answer 1

9 (2/3) ² but insted of 2 its n

Explanation:

Answer 2

The height of a bouncing ball is defined by
`h(n) = 6\cdot \left((4)/(6) \right)^(n-1)`.

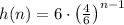Explanation:

According to this statement, we need to derive the expression of the height of a bouncing ball, that is, a function of the number of bounces. The exponential expression of the bouncing ball is of the form:

`h = h_(o)\cdot r^(n-1)`,
`n \in \mathbb{N}`,
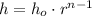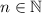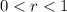`0 < r < 1` (1)

Where:

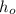`h_(o)` - Height reached by the ball on the first bounce, measured in feet.

`r` - Decrease rate, no unit.

`n` - Number of bounces, no unit.

`h` - Height reached by the ball on the n-th bounce, measured in feet.

The decrease rate is the ratio between heights of two consecutive bounces, that is:

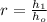`r = (h_(1))/(h_(o))` (2)

Where
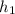`h_(1)` is the height reached by the ball on the second bounce, measured in feet.

If we know that
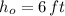`h_(o) = 6\,ft` and
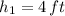`h_(1) = 4\,ft`, then the expression for the height of the bouncing ball is:

`h(n) = 6\cdot \left((4)/(6) \right)^(n-1)`

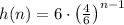
The height of a bouncing ball is defined by
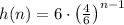`h(n) = 6\cdot \left((4)/(6) \right)^(n-1)`.