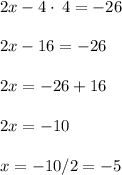Question

Need help ASAP. Need to know how to get x and y from x-2y=-13 and y=-2x-6. Not seperate, the xy for both combined if that makes sense. One answer.

Answer 1

`x = -5\\y = 4`

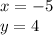
Explanation:

Not sure I understand that part of your question ...not separate, the xy for both combined.

Here are the solution steps to determine x and y values

Given equations are

`\begin{amatrix}x-2y=-13 \dots [1] \\\\ y=-2x-6\dots\dots[2]\end{amatrix}`

In equation [2] get all the variables to the left side and the constant on ther right side:

• Add 2x to both sides of the equation:
  
  `y + 2x = 2x - 2x - 6`
• Simplify:
  
  `y + 2x = - 6`
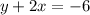
• Rewrite:
  
  `2x+y=-6\dots\dots [3]`

Let's examine equations [1] and [3]:

`\begin{aligned}x - 2y &= - 13 \dots [1]\\ 2x + y &= -6\;\;\dots[3]\\\end{aligned}`

Multiply eq [1],
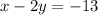`x - 2y = -13` throughout by
`2`:

`2(x - 2y) &= 2(- 13) \implies 2x - 4y = -26 \dots[4]\\`

Subtract the equations:

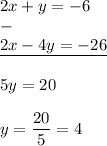
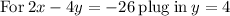`2x+y=-6\\-\\\underline{2x-4y=-26}\\\\5y=20\\\\y = (20)/(5) = 4`

`\mathrm{For\:}2x-4y=-26\mathrm{\:plug\:in\:}y=4`:

`2x-4\cdot \:4=-26\:\\\\2x - 16 = -26\\\\2x = -26 + 16\\\\2x = -10\\\\x = -10/2 = -5`