Question

joe bought a new truck for $45,000. the truck depreciates at a rate of 15% per year. what will be the value of the truck in four years

Answer 1

The value of the truck would be $23,490.28 after 4 years.

Explanation:

Main concepts:

Concept 1. Percentages

Concept 2. Depreciation

Concept 3. Distributive property

Concept 4. Repeated multiplication as a power

Concept 1. Percentages

A percentage is effectively a unit. In the same way that 25¢ is the same as 0.25 US dollars, 15% is the same as 0.15 (unit-less number).

A common task is to find a percentage of a quantity. For example, finding 25% of 40. Mathematically, the word "of" here means multiply, so 25% of 40 means "25% * 40". But, since a percentage can be converted to a regular unit-less number, this is also the same as "0.25 * 40" which is 10. So, 25% of 40 is 10.

Concept 2. Depreciation

To depreciate means that the value of the thing decreases. In this question, the value of the truck depreciates by 15% (per year), so its value would decrease by whatever 15% of its current value is.

15% of $45,000 is 0.15 * $45,000 = $6,750 (this is the amount that the value decreases by during the first year)

To find the value after 1 year, we need to subtract this from the original value. We'll label this equation 1:

• Equation 1: $45,000 - $6,750 = $38,250

Common mistake: It is a common mistake for people to continue subtracting $6,750 for years 2, 3, and 4 thinking that this is subtracting another 15%. However, each year, the 15% depreciation is based on the new value of the truck, so during the second year, the truck started at a value of $38,250 (from the end of the first year), and 15% of $38,250 will be different from 15% of $45,000.

15% of $38,250 is 0.15 * $38,250 = $5,737.50 (this is the amount that the value decreases by)

To find the value after 2 year, we need to subtract this from the value at the end of year 1. We'll label this equation 2:

• Equation 2: $38,250 - $5,737.50 = $32,512.50

Concept 3. Distributive property

In Equation 1 above, the left side of the equation can be factored by using the distributive property in reverse, and factoring out "$45,000":

$45,000 - $6,750 is the same as

$45,000 * ( 1 - 0.15 ) = $38,250 -- Equation 1a

This expression illuminates what is happening to the value if we change the numbers inside the parentheses into percentages

$45,000 * ( 100% - 15% )

Notice that in the parentheses, we start with 100% (whatever 100% is), and we're subtracting 15%.

Similarly, in Equation 2, the left side of the equation can be factored by using the distributive property in reverse, and factoring out "$38,250":

$38,250 - $5,737.50 is the same as

$38,250 * ( 1 - 0.15 ) = $32,512.50 -- Equation 2a

Notice that in the parentheses, we again start with 100% (whatever 100% is), and we're subtracting 15%.

Concept 4. Repeated multiplication as a power

Quick recap from Equation 1a & Equation 2a:

For year 1, Equation 1a: $45,000 * ( 1 - 0.15 ) = $38,250

For year 2, Equation 2a: $38,250 * ( 1 - 0.15 ) = $32,512.50

However, note the equivalence in bold above. This means that we can replace the $38,250 in the "Year 2" equation with the entire left side of the equation from Year 1.

Thus, for Year 2, the equation become:

$45,000 * ( 1 - 0.15 ) * ( 1 - 0.15 ) = $32,512.50

While the value at the end of year 3 could be written

$32,512.50 * ( 1 - 0.15 )

notice that the left side again starts with the value that ended the year before. With another substitution, for Year 3, the equation becomes:

$45,000 * ( 1 - 0.15 ) * ( 1 - 0.15 ) * ( 1 - 0.15 ) = Value at end of year 3

Continuing the pattern, we need the value at the end of the year before, times ( 1 - 0.15 ) to get the value for the end of the following year.

$45,000 * ( 1 - 0.15 ) * ( 1 - 0.15 ) * ( 1 - 0.15 ) * ( 1 - 0.15 ) = Value at end of year 4.

Notice that each year, we're multiplying by another factor of ( 1 - 0.15 )

Recall that multiplying by the same number or expression repeatedly can be simplified with an exponent. For example, five 2s multiplied together: 2*2*2*2*2 can be written as
`2^5`.

Therefore, the value of the truck at the end of year 2 can be written as

`\$45,000 * (1-0.15)^(2)`

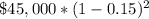
The value of the truck at the end of year 3:
`\$45,000 * (1-0.15)^(3)`

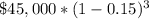
The value of the truck at the end of year 4:
`\$45,000 * (1-0.15)^(4)`

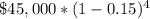
Side note: the value of the truck at the end of any year "n" is
`\$45,000 * (1-0.15)^(n)`

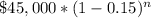
So, to answer the question, and find the value of the truck in 4 years, we just need to evaluate
`\$45,000 * (1-0.15)^(4)`

`\$45,000 * (1-0.15)^(4)=`

`=\$45,000 * (0.85)^(4)`

`=\$45,000 * 0.52200625`

`=\$23,490.28125`

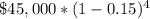
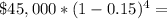
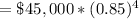
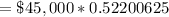
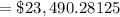
Rounded to the nearest penny, the value of the truck would be $23,490.28 after 4 years.

Answer 2

Explanation:

Each year the truck retains 85 % of its value ( 85% + 15% = 100%)

45000 * .85 * .85 * .85 * .85 = $ 45 000 * .85^4 = $ 23490.28