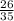Answer:
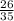
Explanation:
We have four fractions and asked to find the next fraction in the sequence.
The four fractions are increasing one by one by first glance, therefore to find the answer we need to add 1/25 to the last value seen.
What is 1 + 25?
26