To determine the function f(x), we integrate the given derivative f'(x) as follows:


where C is the constant of integration.
To find the value of C, we can use a point of the function. Let's say that f(0) = 5. Then we have:
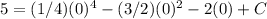
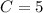
Therefore, the function f(x) is:
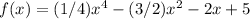
To answer the second question about retirement savings, we need more information about the retirement goals such as the desired retirement income, length of retirement, current age, and expected rate of return. Without this information, we cannot calculate the amount needed to be deposited each year.