Question

Find the lengths of each triangle…
2x ft
6x ft
200ft

Answer 1

`2x=20√(10)\; \textsf{ft} \approx 63.25\; \sf ft`

`6x=60√(10)\; \textsf{ft} \approx 189.74\; \sf ft`

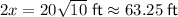
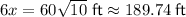
Explanation:

Assuming the given triangle is a right triangle, we can use Pythagoras Theorem to calculate the value of x and then find the measurers of the side lengths.

Pythagoras Theorem

`\large{\boxed{a^2+b^2=c^2}`

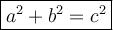
where:

• a and b are the legs of the right triangle.
• c is the hypotenuse (longest side) of the right triangle.

From inspection of the given diagram:

• a = 2x
• b = 6x
• c = 200

Substitute these values into the formula and solve for x.

`\begin{aligned} (2x)^2+(6x)^2&=200^2\\2^2\cdot x^2+6^2\cdot x^2&=40000\\4x^2+36x^2&=40000\\40x^2&=40000\\x^2&=1000\\x&=√(1000)\\x&=√(100 \cdot 10)\\x&=√(100){√(10)\\x&=10√(10)\end{aligned}`

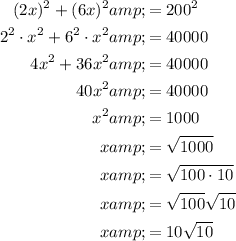
Substitute the found value of x into the expression for each side length.

`2x=2 \cdot 10√(10)=20√(10)`

`6x=6\cdot 10√(10)=60√(10)`

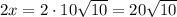
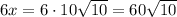
Therefore, the exact side lengths of the given right triangle are:

`20√(10)\; \textsf{ft}, \;\;60√(10)\; \textsf{ft}, \;\; 200\; \textsf{ft}`

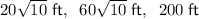
The side lengths to the nearest hundredth are:

• 63.25 ft
• 189.74 ft
• 200 ft