Question

How do i find the inverse

Answer 1

Answer:
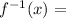`f^(-1)(x) =` x²-10x+19

Explanation:

Let's replace f(x) for y for now.

`y=√(x-6)+5`

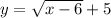
To find inverse. make your y into x, and your x into y

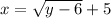`x=√(y-6)+5` >Now you solve for y. subtract 5 from both sides

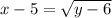`x-5=√(y-6)` >Square both sides to get rid of root

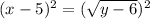`(x-5)^(2) =(√(y-6))^(2)` >drop root and square (x-5)

(x-5)(x-5) = y-6 >FOIL

x²-5x-5x+25 = y-6 > combine like terms

x²-10x+25 = y-6 >add 6 to both sides

x²-10x+19=y > this is your inverse now put the y into inverse form

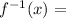`f^(-1)(x) =` x²-10x+19

Answer 2

Explanation:

To solve for inverse, utilize the following steps.

Step 1: let f(x)=y so we get

`y = √(x - 6) + 5`

Step 2: Swap y and x

`x = √(y - 6) + 5`

Solve for y.

`x - 5 = √(y - 6)`

`(x - 5) { }^(2) + 6 = y`

Step 4: Let y =f^-1(x)

`(x - 5) {}^(2) + 6 = f {}^( - 1) (x)`