Question

O is the center of the regular hexagon below. Find its area. Round to the nearest tenth if necessary

Answer 1

The area of the regular hexagon is 509.2 square units (to the nearest tenth).

The formula for the area of a regular polygon is:

`\boxed{\text{Area}=\frac{\text{r}^2\text{n sin}\huge \text(\frac{360^\circ}{\text{n}}\huge \text) }{y} }`

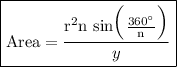
where:

• r is the radius (the distance from the center to a vertex).
• n is the number of sides.

From inspection of the given regular polygon:

• r = 14 units
• n = 6

Substitute the values into the formula and solve for area:

`\text{Area}=\frac{14^2*6*\text{sin}\huge \text((360^\circ)/(6)\huge \text) }{2}`

`=\frac{196*6*\text{sin} (60^\circ)}{2}`

`=(1176*(√(3) )/(2) )/(2)`

`=(588√(3) )/(2)`

`=294√(3)`

`=509.2 \ \text{square units (nearest tenth)}`

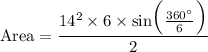
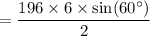
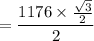
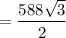
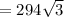
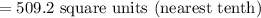
Therefore, the area of the regular hexagon is 509.2 square units (to the nearest tenth).