Question

Please I am so close to being done with this assignment I rly rly need this

Answer 1

(-2, -7)

Explanation:

The second equation is already arranged in such a way that allows us to substitute it for x in the first equation, which will then allow us to solve for y:

`-4x+7y=-41\\x=y+5\\\\-4(y+5)+7y=-41\\-4y-20+7y=-41\\3y-20=-41\\3y=-21\\y=-7`

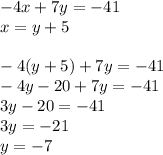
Now, we can plug in -7 for y in any of the two original equations. We can do the second one since it's' the simplest of the two:

`x=-7+5\\x=-2`

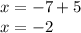
Finally, we can check our answers by plugging in -2 for x and -7 for y in both the equations and check that we get -41 for the first equation and -2 for the second equation.

Checking solutions for first equation:

-4(-2) + 7(-7) = -41

8 - 49 = -41

-41 = -41

Checking solutions for second equation:

-2 = -7 + 5

-2 = -2