Question

Determine whether y=3x^2 - 12x + 1 has a minimum or a maximum value. Then find the value

Answer 1

Minimum

-11

Explanation:

Main concepts:

Concept 1: Identify the type of equation

Concept 2: Identify the concavity (opens up/down)

Concept 3: Finding a vertex of a parabola

Concept 1: Identify the type of equation

First, observe that the equation is a polynomial. This is a type of equation where there may be multiple terms containing an x, where each term with an x is raised to a whole number power, and may be multiplied by a real number. Additionally, there may be a constant term added (or subtracted).

For our equation,
`y=3x^2-12x+1`, the first two terms contain an x, each raised to a whole number power, and are multiplied by a number. Additionally, there is a constant added to the end of the equation. Therefore, this is a polynomial.

The largest power of x in a polynomial is called the "degree" of the polynomial. Since the largest power of x is 2, this is called a second degree polynomial. Another common name for a second degree polynomial is a quadratic equation.

This quadratic equation is already in what is known as "Standard form"
`y=ax^2+bx+c`

Concept 2: Identify the concavity (opens up/down)

For quadratic equations, the graph of the equation will be a sort of "U" shape" called a parabola. The parabola either opens up or down depending on the "leading coefficient" in the quadratic equation.

The "leading coefficient" of any polynomial is the constant number that is multiplied to x in the term with the highest power. In this case, the leading coefficient is 3.

A parabola opens up or down in correspondence with the sign of the leading coefficient. If the leading coefficient is positive, the parabola opens upward. If the leading coefficient is negative, the parabola opens downward.

Since the leading coefficient is 3, the parabola for our example opens upward. The branches of the "U" will go upward forever, without a maximum. However, the bottom of the "U" will have a minimum value. We are assigned to find this minimum value (how low it goes).

Concept 3: Finding a vertex of a parabola

To find the vertex of a parabola, with an equation in standard form, there are a few methods, but the most straightforward is to use the vertex formula:

`h=(-b)/(2a)`

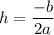
Where "h" is the x-coordinate of the vertex, and "a" and "b" are the coefficients from the quadratic equation:
`y=ax^2+bx+c`

`h=(-(-12))/(2(3))`

`h=(12)/(6)`

`h=2`

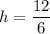
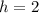
So, the parabola will have a vertex with an x-coordinate of "2", meaning that the lowest point will be at a position that is 2 units to the right of the origin... however, we still don't know how high that minimum is. Fortunately, the equation
`y=3x^2-12x+1` itself gives the relationship between any x-value and the y-value that is associated with it.

`y=3x^2-12x+1`

`y=3(2)^2-12(2)+1`

`y=3*4+(-12)*2+1`

`y=12+-24+1`

`y=-11`

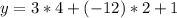
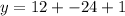
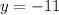
So, the vertex of the parabola is (2,-11).

The height of the vertex is -11, so the value of the minimum is -11.

Side note: "What is the value of the minimum" is a different question that "where is the minimum at". The minimum is at 2. The actual value of the minimum is -11.