Question

Penelope invested $89,000 in an account paying an interest rate of 6 1/4% compounded continuously. Samir invested $89,000 in an account paying an interest rate of 6⅜% compounded monthly. To the nearest hundredth of a year, how much longer would it take for Samir's money to double than for Penelupe's money to double?

Answer 1

Answer: -10.57

Explanation:

Answer 2

0.25 years

Explanation:

Penelope invested $89,000 in an account paying an interest rate of 6⅜% compounded continuously.

To calculate the time it would take Penelope's money to double, use the continuous compounding interest formula.

`\boxed{\begin{minipage}{8.5 cm}\underline{Continuous Compounding Interest Formula}\\\\$ A=Pe^(rt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\\phantom{ww}$\bullet$ $P =$ principal amount \\\phantom{ww}$\bullet$ $e =$ Euler's number (constant) \\\phantom{ww}$\bullet$ $r =$ annual interest rate (in decimal form) \\\phantom{ww}$\bullet$ $t =$ time (in years) \\\end{minipage}}`

As the principal amount is doubled, then A = 2P.

Given interest rate:

• r = 6.375% = 0.06375

Substitute A = 2P and r = 0.06375 into the continuous compounding interest formula and solve for t:

`\implies 2P=Pe^(0.06375t)`

`\implies 2=e^(0.06375t)`

`\implies \ln 2=\ln e^(0.06375t)`

`\implies \ln 2=0.06375t\ln e`

`\implies \ln 2=0.06375t(1)`

`\implies \ln 2=0.06375t`

`\implies t=(\ln 2)/(0.06375)`

`\implies t=10.872896949...`

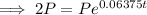
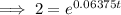
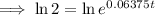
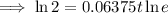
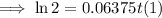
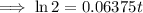
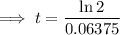
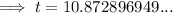
Therefore, it will take 10.87 years for Penelope's investment to double.

`\hrulefill`

Samir invested $89,000 in an account paying an interest rate of 6¹/₄% compounded monthly.

To calculate the time it would take Samir's money to double, use the compound interest formula.

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

As the principal amount is doubled, then A = 2P.

Given values:

• A = 2P
• P = P
• r = 6.25% = 0.0625
• n = 12 (monthly)

Substitute the values into the formula and solve for t:

`\implies 2P=P\left(1+(0.0625)/(12)\right)^(12t)`

`\implies 2=\left(1+(0.0625)/(12)\right)^(12t)`

`\implies 2=\left(1+0.005208333...\right)^(12t)`

`\implies 2=\left(1.005208333...\right)^(12t)`

`\implies \ln 2=\ln \left(1.005208333...\right)^(12t)`

`\implies \ln 2=12t \ln \left(1.005208333...\right)`

`\implies t=(\ln 2)/(12 \ln \left(1.005208333...\right))`

`\implies t=11.1192110...`

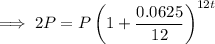
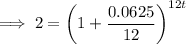
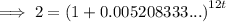
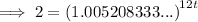
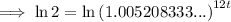
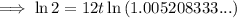
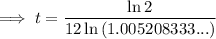
Therefore, it will take 11.12 years for Samir's investment to double.

`\hrulefill`

To calculate how much longer it would take for Samir's money to double than for Penelope's money to double, subtract the value of t for Penelope from the value of t for Samir:

`\begin{aligned}\implies t_(\sf Samir)-t_(\sf Penelope)&=11.1192110......-10.872896949...\\&= 0.246314066...\\&=0.25\; \sf years\;(nearest\;hundredth)\end{aligned}`

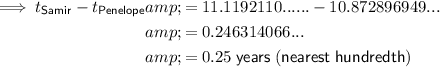
Therefore, it would take 0.25 years longer for Samir's money to double than for Penelope's money to double.