Question

Wayne Gretzky was gliding at 2.00 m/s [W] when he collided with Joel Otto who was gliding at 1.80 m/s [E]. After the head on collision, Gretzky ends up going at 1.00 m/s [E] and Otto at 0.100 m/s [E]. What is the ratio of the mass of Gretzky to the mass of Otto?

Answer 1

Mass of Otto is approximately
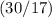`(30 / 17)` times that of Gretzky.

Step-by-step explanation:

Let
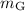`m_{\text{G}}` and
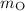`m_{\text{O}}` denote the mass of Gretzky and Otto. Let
`u_{\text{G}}` and
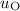`u_{\text{O}}` denote their velocity before the collision. Let
`v_{\text{G}}` and
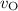`v_{\text{O}}` denote their velocity after the collision.

By the conservation of momentum:

`m_{\text{G}}\, u_{\text{G}} + m_{\text{O}}\, u_{\text{O}} = m_{\text{G}}\, v_{\text{G}} + m_{\text{O}}\, v_{\text{O}}`.

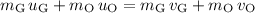Assume that
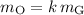`m_{\text{O}} = k\, m_{\text{G}}` for some constant
`k > 0` denoting the ratio of mass between Otto and Gretzky. The equation for the conservation of momentum becomes:

`m_{\text{G}}\, u_{\text{G}} + (k\, m_{\text{G}})\, u_{\text{O}} = m_{\text{G}}\, v_{\text{G}} + (k\, m_{\text{G}})\, v_{\text{O}}`.

`u_{\text{G}} + k\, u_{\text{O}} = v_{\text{G}} + k\, v_{\text{O}}`.

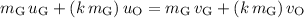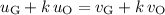Rearrange and solve for the ratio
`k`:

`\begin{aligned}(v_{\text{O}} - u_{\text{O}})\, k = u_{\text{G}} - v_{\text{G}} \end{aligned}`.

`\begin{aligned}k = \frac{u_{\text{G}} - v_{\text{G}}}{v_{\text{O}} - u_{\text{O}}} \end{aligned}`.

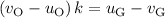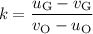Let the East be the positive direction. Since it is given that the initial velocity of Gretzky is opposite to the East, the initial velocity of Gretzky would be negative:
`u_{\text{G}} = (-2.00)\; {\rm m\cdot s^(-1)}`.

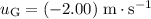It is also given that
`u_{\text{O}} = 1.80\; {\rm m\cdot s^(-1)}`,
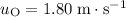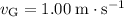`v_{\text{G}} = 1.00\; {\rm m\cdot s^(-1)}`, and
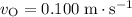`v_{\text{O}} = 0.100\; {\rm m\cdot s^(-1)}`. Substitute these values into the equation to find the ratio
`k`:

`\begin{aligned}k &= \frac{u_{\text{G}} - v_{\text{G}}}{v_{\text{O}} - u_{\text{O}}} \\ &= ((-2.00) - 1.00)/(0.100 - 1.80) \\ &= (30)/(17)\end{aligned}`.

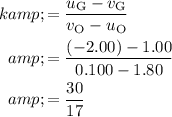In other words, the mass of Otto was
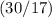`(30 / 17)` times that of Gretzky.