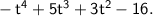Question

Subtract t⁴-3t²+7 from 5t³-9.​

Answer 1

t⁴+5t³-3t²-2

Explanation:

You can't subtract a variable with a different exponent:

Example:

CAN'T BE SUBTRACTED - 3x²-3x⁴

CAN BE SUBTRACTED - 4x²-2x²=2x²

Answer 2

`\sf -t^(4)+5t^(3) +3t^(2) -16.`

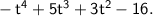
Explanation:

1. Write the expression.

`\sf (5t^(3) -9)-(t^(4)-3t^(2) +7 )`

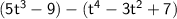
2. Remove the parenthesis.

Beware of the terms of the right hand side parenthesis, as we'll have to change the symbol of all of them because of the minus (-) symbol infront of the parenthesis.

`\sf 5t^(3) -9-t^(4)+3t^(2) -7`

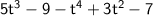
3. Work with like terms.

Like terms are terms that contain the same variables and can be added and subtracted simply. For example, 7x and 2x are like terms, because they are both expressed in terms of x. However, 7x and x² are not like terms, because one os expressed in terms of x and the ither in terms of x².

• Note: All natural numbers not being multiplied by any variables are like terms.

So now let's identify those like terms:

From this expression:
`\sf 5t^(3) -9-t^(4)+3t^(2) -7`

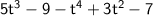
Only -9 and -7 are like terms. And, since -9-7= -16, the resulting expression should be the following:

`\sf 5t^(3) -t^(4)+3t^(2) -16`

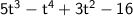
4. Order the terms correctly.

So even though the last expression is the answer to this problem, we can polish it a little bit by ordering the terms. In math and other exact sciences, terms are normally ordered alphabetically and from greatest to least of it's the same variable with different exponents. Therefore, the final answer is:

`\sf -t^(4)+5t^(3) +3t^(2) -16.`