Question

14). Find the measures of both angles.
xo
(3x +20)°

Answer 1

40 degrees and 140 degrees

Explanation:

To solve this problem you can add x+3x+20 and set that equal to 180. (We can do this because angle x and angle 3x + 20 make a linear pair. Knowing this we can estimate that both angles added together will equal 180)

Let us add x + 3x + 20 = 180 to find x. We can then substitute that into the equation.

`x+3x+20=180 :a\\\\4x+20=180 :b\\\\4x + 20 -20=180-20:c\\\\4x=160:d\\\\(4x)/(4) = (160)/(4):e\\\\x=40:f`

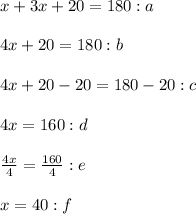
a: So in this part, we have rewritten the equation to make it easier to solve

b: In this step, you combine the like terms x+3x to get 4x

c: In step c, you are subtracting 20 from both sides to keep constants on one side and variables on the right

d: In this last step the equation has been simplified to make it easier to solve.

e: To isolate x you have to divide both sides by 4, we do this because the coefficient of x is 4 so you divide the equation by 4 to cancel it out.

f: You rewrite and simplify the equation.

Now to find the measure of both angles you substitute x into the equation.

The first angle's value is 40 degrees and the second is 140 degrees.

These are our answers.