Question

PLEASE HELP! Showing all work, solve for x and why and round to nearest tenth

Answer 1

x = 7.9 (nearest tenth)

y = 24.6° (nearest tenth)

Explanation:

Pythagoras Theorem explains the relationship between the three sides of a right triangle. The square of the hypotenuse (longest side) is equal to the sum of the squares of the legs of a right triangle.

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

As we have been given the lengths of both legs of the right triangle, we can use Pythagoras Theorem to find the length of the hypotenuse, x:

`\begin{aligned}3.2^2+7^2&=x^2\\10.24+49&=x^2\\59.24&=x^2\\x^2&=59.24\\x&=√(59.24)\\x&=7.6967525...\\x&=7.9\; \sf (nearest\;tenth)\end{aligned}`

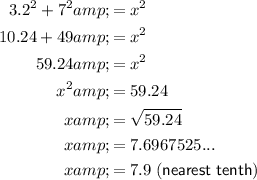
Therefore, x = 7.9.

`\hrulefill`

The tangent ratio is a trigonometric ratio that relates the angle of a right triangle to the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

As we have been given the lengths of the sides that are opposite and adjacent angle y, we can use the tangent trigonometric ratio to find the measure of angle y:

`\begin{aligned}\tan(y)&=(3.2)/(7)\\y&=\tan^(-1)\left((3.2)/(7)\right)\\y&=\vphantom{\frac12}24.5671713...^(\circ)\\y&=24.6^(\circ)\;\sf (nearest\;tenth)\end{aligned}`

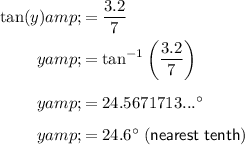
Therefore, y = 24.6°.