Question

A construction company will be penalized each day of delay in construction for bridge. The penalty will be $4000 for the first day and will increase by $10000 for each following day. Based on its budget, the company can afford to pay a maximum of $ 165000 toward penalty. Find the maximum number of days by which the completion of work can be delayed.

Answer 1

The answer toy our problem is, The maximum number of days by which the completion of work can be delayed is 15.

Explanation:

We are given that the penalty amount paid by the construction company from the first day as sequence, 4000, 5000, 6000, ‘ and so on ‘. The company can pay 165000 as penalty for this delay at maximum that is

`S_(n)`​ = 165000.

Let us find the amount as arithmetic series as follows:

4000 + 5000 + 6000

The arithmetic series being, first term is
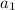`a_(1)` = 4000, second term is
`a_(2)` = 5000.

We would have to find our common difference ‘ d ‘ by subtracting the first term from the second term as shown below:

`d = a_(2) - a_(1) = 5000 - 4000 = 1000`

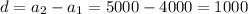
The sum of the arithmetic series with our first term ‘ a ‘ which the common difference being,
`S_(n) = (n)/(2) [ 2a + ( n - 1 )d ]` ( ‘ d ‘ being the difference. )

Next we can substitute a = 4000, d = 1000 and
`S_(n)` = 165000 in “
`S_(n) = (n)/(2) [ 2a + ( n - 1 )d ]` “ which can be represented as:

Determining,
`S_(n) = (n)/(2) [ 2a + ( n - 1 )d ]`

⇒ 165000 =
`(n)/(2)` [( 2 x 4000 ) + ( n - 1 ) 1000 ]

⇒ 2 x 165000 = n(8000 + 1000n - 1000 )

⇒ 330000 = n(7000 + 1000n)

⇒ 330000 = 7000n +
`1000n^2`

⇒
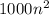
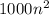`1000n^2` + 7000n - 330000 = 0

⇒
`1000n^2` (
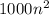`n^2` + 7n - 330 ) = 0

⇒
`n^2` + 7n - 330 = 0

⇒
`n^2` + 22n - 15n - 330 = 0

⇒ n( n + 22 ) - 15 ( n + 22 ) = 0

⇒ ( n + 22 )( n - 15 ) = 0

⇒ n = -22, n = 15

We need to ‘ forget ‘ the negative value of ‘ n ‘ which will represent number of days delayed, therefore, we get n=15.

Thus the answer to your problem is, The maximum number of days by which the completion of work can be delayed is 15.