Question

during an evacuation drill, people leave a building at a rate of r t( ) people per minute, where t is the number of minutes since the start of the drill. selected values of r t( ) are shown in the table above. using a right riemann sum with three subintervals and data from the table, what is the approximation of the number of people who leave the building during the first 15 minutes of the evacuation drill?

Answer 1

To find the approximation of the number of people who leave the building during the first 15 minutes, we need to calculate the sum of the products of the rate and the width of each subinterval using a right Riemann sum with three subintervals.

Step-by-step explanation:

To find the approximation of the number of people who leave the building during the first 15 minutes of the evacuation drill using a right Riemann sum with three subintervals, we need to calculate the sum of the products of the rate and the width of each subinterval.

The width of each subinterval is (15/3) = 5 minutes.

The values of the rate function are given in the table. We need to evaluate the rate function at the right endpoints of each subinterval and multiply it by the width of the subinterval.

Summing up the products, we get: (r(5) * 5) + (r(10) * 5) + (r(15) * 5).

Answer 2

The approximation of the number of people leaving the building in the first 15 minutes using a Right Riemann sum with three subintervals is 1150.

Use the Right Riemann Sum to approximate the number of people who leave the building during the first 15 minutes of the evacuation drill using the provided data:

Given values:

- t values: 0, 5, 10, 15 (in minutes)

- R(t) values: 100, 100, 75, 55 (people per minute)

The Right Riemann Sum formula for approximation is:

`\[\text{Sum} = \Delta t \cdot \left[f(t_1) + f(t_2) + f(t_3)\right]\]`

Where:

-
`\(\Delta t\)` is the width of each subinterval.

-
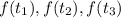`\(f(t_1), f(t_2), f(t_3)\)` are the values of R(t) at the right endpoints of the subintervals.

Given:

-
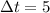`\(\Delta t = 5\)` minutes (since the intervals are of length 5 minutes)

-
`\(f(t_1) = R(5) = 100\) (at \(t = 5\) minutes)`

-
`\(f(t_2) = R(10) = 75\) (at \(t = 10\) minutes)`

-
`\(f(t_3) = R(15) = 55\) (at \(t = 15\) minutes)`

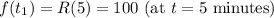
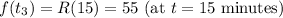
Now, let's calculate the Right Riemann Sum:

`\[\text{Sum} = 5 \cdot \left[100 + 75 + 55\right]\]`

`\[\text{Sum} = 5 \cdot 230\]`

`\[\text{Sum} = 1150\]`

Therefore, the approximation of the number of people who leave the building during the first 15 minutes of the evacuation drill using the Right Riemann Sum with three subintervals is 1150, which corresponds to option (b).

Question:

t(minutes) 0 5 10 15

R(t) (people per minute) 100 100 75 55

During an evacuation drill, people leave a building at a rate of R (t) people per minute, where t is the number of minutes since the start of the drill. selected values of R (t) are shown in the table above. Using a right Riemann sum with three subintervals and data from the table, what is the approximation of the number of people who leave the building during the first 15 minutes of the evacuation drill?

a. 230

b. 1150

c. 1375

d. 2075