Question

Following the steps below, use logarithmic differentiation to determine the derivative of the function f(x)= (1+2x)^1/x / sin(x)

a. Take the natural log of both sides and use properties of logarithms to expand the function: ln(f(x))=ln((1+2x)^(x1)csc(x)) b. Take the derivative implicitly: f(x)/f (x) = c. Solve for f ' (x) and replace f(x) with the original function definition: f' (x)=

Answer 1

a. Taking the natural log on both sides,
`In(f(x))=(In (1+2x) )/(x) - In \ sin (x) }`

b. Taking the derivative implicitly, we have:
`(f'(x))/(f(x))=-(In(1+2x))/(x^2)+(2)/(x(1+2x))-cot (x)`

c.
`f'(x) =((1+2x)^(1/x))/(sin (x)) \Big [ -(In (1+2x))/(x^2)+(2)/(x(1+2x))-cot (x) \Big]`

Calculating the derivative of a function

The derivative of the given function can be calculated by following the step-by-step process.

Given that:

`f(x)=((1+2x)^(1/x))/(sin(x))`

We use the logarithm properties to expand the function, and take the natural log (㏑) on both sides; we have:

`In(f(x))=In \Big( ((1+2x)^(1/x))/(sin (x) ) \Big)`

`In(f(x))=In ((1+2x)^(1/x) - In \ sin (x) }`

`In(f(x))=(1)/(x) In ((1+2x) - In \ sin (x) }`

`In(f(x))=(In (1+2x) )/(x) - In \ sin (x) }`

b.
`In(f(x))=(In (1+2x) )/(x) - In \ sin (x) }`

Taking the implicit derivative corresponding to x;

`(d)/(dx)In(f(x))= (d)/(dx)\Big ((In (1+2x) )/(x) - In \ sin (x) } \Big )`

`(1)/(f(x))(d)/(dx)f(x) =(d)/(dx)(In(1+2x)x^(-1))-(d)/(dx) In sin(x))`

By implementing the product rule;

`(1)/(f(x))f'(x) = In (1+2x) (d)/(dx)x^(-1)+x^(-1) (d)/(dx)In (1+2x) -(1)/(sin (x))(d)/(dx)(sin(x))`

`(1)/(f(x))f'(x) = In (1+2x) (-x^(-2)) + (x^(-1))/(1+2x)(d)/(dx)(1+2x)-(1)/(sin (x))(cos (x))`

`(1)/(f(x))f'(x)=-(In(1+2x))/(x^2)+(1)/(x(1+2x))(2)-cot(x)`

`(f'(x))/(f(x))=-(In(1+2x))/(x^2)+(2)/(x(1+2x))-cot (x)`

c. Solving for f'(x) and replacing f(x) with the original function, we have:

`f'(x) = f(x) \Big [ -(In(1+2x))/(x^2)+(2)/(x(1+2x))-cot (x) \Big]`

provided that:
`f(x) = ((1+2x)^(1/x))/(sin (x))`, then:

`f'(x) =((1+2x)^(1/x))/(sin (x)) \Big [ -(In (1+2x))/(x^2)+(2)/(x(1+2x))-cot (x) \Big]`

Answer 2

The derivative of the function
`\(f(x) = ((1+2x)^(1/x))/(\sin(x))\) is given by \(f'(x) = ((1+2x)^(1/x))/(\sin(x)) \cdot \left((1)/(x) - \ln(1+2x) -`\cot(x)\right)\). This expression reflects the rate of change of the original function, incorporating the intricate interplay of exponential, logarithmic, and trigonometric components.

Step-by-step explanation:

To find the derivative of the given function
`\(f(x) = ((1+2x)^(1/x))/(\sin(x))\)`, we'll use logarithmic differentiation.

1. Take the natural log:

Start by taking the natural logarithm of both sides:

`\[\ln(f(x)) = \ln\left((1+2x)^(1/x) \cdot \csc(x)\right)\]`

2. Expand using properties of logarithms:

Apply logarithmic properties to expand the expression:

`\[\ln(f(x)) = (1)/(x) \cdot \ln(1+2x) - \ln(\sin(x))\]`

3. Take the derivative implicitly:

Differentiate both sides implicitly with respect to
`\(x\)`:

`\[(f'(x))/(f(x)) = (1)/(x) - (1)/(\sin(x)) - \cot(x)\]`

4. Solve for
`\(f'(x)\)`:

Solve for
`\(f'(x)\)` by multiplying both sides by
`\(f(x)\)` and replacing
`\(f(x)\)`with the original function:

`\[f'(x) = ((1+2x)^(1/x))/(\sin(x)) \cdot \left((1)/(x) - \ln(1+2x) - \cot(x)\right)\]`

The natural logarithm allows us to simplify the expression by using logarithmic properties. Taking the derivative implicitly involves differentiating each term on both sides. The result is an expression for
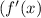`(f'(x)\)` in terms of the original function
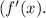`(f'(x)\).` The key steps include recognizing the chain rule and logarithmic differentiation principles. The final expression captures the rate of change of the given function with respect to
`\(x\)`, incorporating the intricacies of the original function's structure.