Question

Solve for x and graph the solution on the number line below.

Answer 1

`-6\leq x < 5`

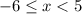
Explanation:

Given compound inequality:

`31 \geq-4x+7\;\;\;\textsf{and}\;\;\;-4x+7 > -13`

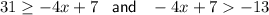
Solve the first inequality:

`\begin{aligned}31 & \geq -4x+7\\\\31 +4x& \geq -4x+7+4x\\\\4x+31& \geq 7\\\\4x+31-31 & \geq 7-31\\\\4x & \geq -24\\\\(4x)/(4) & \geq (-24)/(4)\\\\x & \geq -6\end{aligned}`

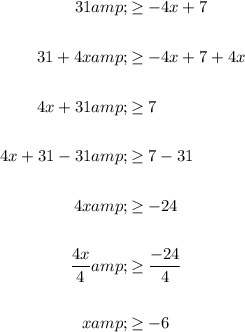
Solve the second inequality:

`\begin{aligned}-4x+7& > -13\\\\-4x+7-7& > -13-7\\\\-4x& > -20\\\\(-4x)/(-4)& > (-20)/(-4)\\\\x& < 5\end{aligned}`

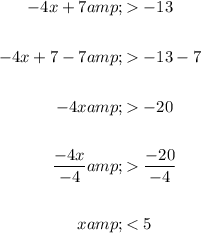
Therefore, combining the solutions, the solution to the compound inequality is:

`\large\boxed{-6\leq x < 5}`

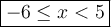
When graphing inequalities:

• < or > : open circle.
• ≤ or ≥ : closed circle.
• < or ≤ : shade to the left of the circle.
• > or ≥ : shade to the right of the circle.

To graph the solution:

• Place a closed circle at x = -6.
• Place an open circle at x = 5.
• Connect the circles with a line.