Question

What is the length of side AC, to the nearest tenth of a unit?

- 13.5 units

- 6.6 units

- 16.7 units

- 30.8 units

Answer 1

• 13.5 units

Step-by-step Step-by-step explanation:

In the given figure,

• AB (Hypotenuse) = 15 units
• AC (Perpendicular) = ?

We know that,

`: \implies \rm(P)/(H)= sin \theta \\`

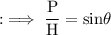
where,

P is perpendicular (AC)

H is Hypotenuse (AB)

`\theta` is 64°

Substituting the values,

`: \implies \sf (AC)/(15) = sin \: 65\degree`

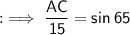
sin 65 = 0.9063 (approximately)

`:\implies \sf (AC)/(15) = 0.9063 \\`

`:\implies \sf AC = 0.9063 * 15 \\`

`:\implies \sf AC \approx 13.59 \\`

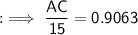
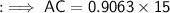
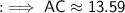
Therefore, the length of side AC is 13.5 units