Answer:
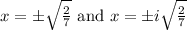
(real solution) (imaginary solution)
Explanation:
Substitution:
For these type of questions, where the exponent is even, it helps to try to rewrite the equation into a quadratic equation as we have a closed formula (quadratic formula) to solve for the zeroes, and it's also just easier to deal with in general.
Let's say that:
 , now if we square both sides,
, now if we square both sides,
 , so from here we can substitute in u squared as x to the power of four.
, so from here we can substitute in u squared as x to the power of four.
This results in our following equation:
 , from here we could use the quadratic formula, but you may notice a pattern here. We have a difference of squares:
, from here we could use the quadratic formula, but you may notice a pattern here. We have a difference of squares:
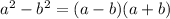
 can be written as
can be written as
 and
and
 can be written as
can be written as
 , this gives us our equation:
, this gives us our equation:
 . If we use this definition of the equation on the left side, it gives us:
. If we use this definition of the equation on the left side, it gives us:
 and this is very convenient as we can solve both of them individually.
and this is very convenient as we can solve both of them individually.
Zero Property of Multiplication:
Whenever we multiply any number (assuming it's defined) by zero, we should get.... zero. This intuitively makes sense as no matter how many times we add zero up (multiplication is repeated addition), we're always just going to have zero.
So when we have the equation:
 , if "a" is zero then regardless of what "b" is (assuming it's defined), then the product will be zero. If "b" is zero then regardless of what "a" is (assuming it's defined), then the product will be zero.
, if "a" is zero then regardless of what "b" is (assuming it's defined), then the product will be zero. If "b" is zero then regardless of what "a" is (assuming it's defined), then the product will be zero.
Now if we look back at our equation:
 , if
, if
 , then regardless of what
, then regardless of what
 is equal to, the product will be zero. Likewise, if
is equal to, the product will be zero. Likewise, if
 then regardless of what
then regardless of what
 is equal to, the product will be zero, thus making the equation true.
is equal to, the product will be zero, thus making the equation true.
So to find the solutions to this, we find what makes
 true. If we work them both out individually we
true. If we work them both out individually we
get:
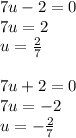
So now we have our two solutions right? Well remember we started off with a "x" variable, and the "u" is merely a substitution. If you recall, the "u" value is set equal to "x^2", so we can just plug that back in, so we can find the solutions in terms of x.
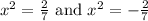
If we take the square root of both sides, we get:

you'll notice in one of them, we're taking the square root of a negative number. This will result in imaginary solutions, if we factor out a "-1" and take the square root of that, we'll just get an "i" infront, giving us the solutions of:
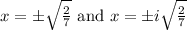 .
.