Question

Rewrite y(x)=2(x-3)^2-9 standard form

Answer 1

The standard form of the given equation is y(x) = 2x² - 12x + 9.

Explanation:

To rewrite the equation y(x) = 2(x-3)² - 9 in standard form, we need to expand the square term (x-3)², simplify the expression, and arrange the terms in descending order of degree.

First, we can expand the square term using the formula (a-b)² = a² - 2ab + b². In this case, a = x and b = 3, so we have:

`\begin{aligned}\sf:\implies (x-3)^2& =\sf x^2 - 2(3)x + 3^2\\& =\sf x^2 - 6x + 9\end{aligned}`

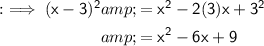
Substituting this expression into the original equation, we get:

`\sf:\implies y(x) = 2(x^2 - 6x + 9) - 9`

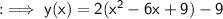
Next, we can simplify the expression by distributing the 2:

`\sf:\implies y(x) = 2x^2 - 12x + 18 - 9`

`\sf:\implies y(x) = 2x^2 - 12x + 9`

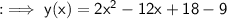
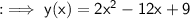
Finally, we can rearrange the terms in descending order of degree (highest power of x first):

`\sf:\implies y(x) = 2x^2 - 12x + 9`

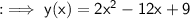
Therefore, the standard form of the given equation is y(x) = 2x² - 12x + 9.

Greetings! ZenZebra at your service, hope it helps! <33